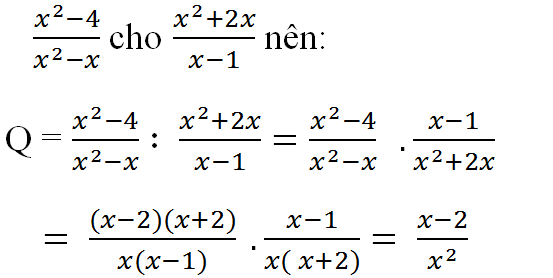\(\dfrac{x^2 + 2x}{x - 1} . Q = \dfrac{x^2 - 4}{x^2 - x}\)
Vì \(Q\) là thương của phép chia \(\dfrac{x^2 - 4}{x^2 - x}\) cho \(\dfrac{x^2 + 2x}{x - 1}\)nên,
Ta có : \(Q = \) \(\dfrac{x^2-4}{x^2-x}:\dfrac{x^2+2x}{x-1}\)
\(Q = \) \(\dfrac{x^2-4}{x^2-x}.\dfrac{x-1}{x^2+2x}\)
\(Q =\) \(\dfrac{\left(x-2\right)\left(x+2\right).\left(x-1\right)}{x\left(x-1\right).x\left(x+2\right)}\) \(=\) \(\dfrac{x-2}{x^2}\)
\(\dfrac{x^2+2x}{x-1}\cdot Q=\dfrac{x^2-4}{x^2-x}\)
\(=>Q=\dfrac{x^2-4}{x^2-x}:\dfrac{x^2+2x}{x-1}\)
\(=>Q=\dfrac{x^2-4}{x^2-x}\cdot\dfrac{x-1}{x^2+2x}\)
\(=>Q=\dfrac{\left(x-2\right)\cdot\left(x+2\right)\cdot\left(x-1\right)}{x\left(x-1\right)\cdot x\left(x+2\right)}\)
\(=>Q=\dfrac{x-2}{x^2}\)
\(\dfrac{x^2-4}{x^2-x}\)cho\(\dfrac{x^2+2x}{x-1}\)nên ta có:
Q = \(\dfrac{x^2-4}{x^2-x}\):\(\dfrac{x^2+2x}{x^2-x}\)=\(\dfrac{x^2-4}{x^2-x}\).\(\dfrac{x-1}{x^2+2x}\)
=\(\dfrac{\left(x-2\right)\left(x+2\right)}{x\left(x-1\right)}\).\(\dfrac{x-1}{x\left(x+2\right)}\)=\(\dfrac{x-2}{x^2}\)