o) Ta có: \(\left(\dfrac{1}{\sqrt{5}-2}-\dfrac{59}{3\sqrt{7}-2}\right)\left(\sqrt{5}+3\sqrt{7}\right)\)
\(=\left(\sqrt{5}+2-3\sqrt{7}-2\right)\left(\sqrt{5}+3\sqrt{7}\right)\)
\(=\left(\sqrt{5}-3\sqrt{7}\right)\left(\sqrt{5}+3\sqrt{7}\right)\)
=5-63=-58
p) Ta có: \(\left(\dfrac{9-2\sqrt{14}}{\sqrt{7}-\sqrt{2}}\right)^2+\left(\dfrac{9+2\sqrt{14}}{\sqrt{7}+\sqrt{2}}\right)^2\)
\(=\left(\sqrt{7}-\sqrt{2}\right)^2+\left(\sqrt{7}+\sqrt{2}\right)^2\)
\(=9-2\sqrt{14}+9+2\sqrt{14}\)
=18
q) Ta có: \(\left(\dfrac{\sqrt{7}-\sqrt{14}}{1-\sqrt{2}}+\dfrac{\sqrt{15}-\sqrt{5}}{1-\sqrt{3}}\right):\dfrac{1}{\sqrt{7}+\sqrt{5}}\)
\(=\left(\sqrt{7}-\sqrt{5}\right)\cdot\left(\sqrt{7}+\sqrt{5}\right)\)
=7-5=2
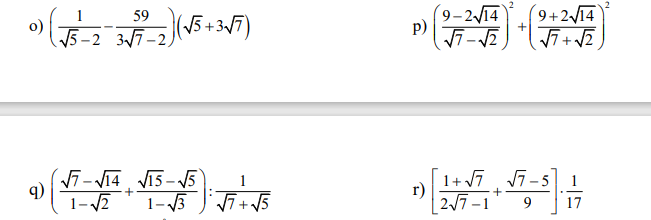
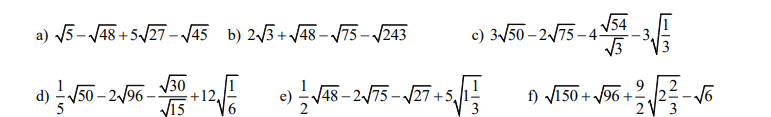
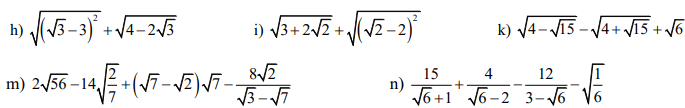
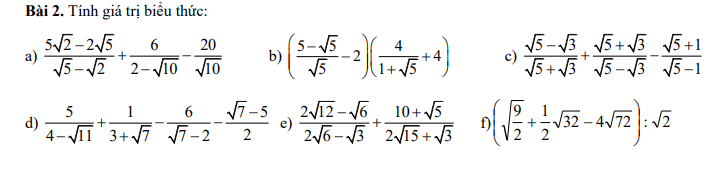
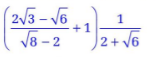
với x ³ 0 và x ¹ 1.
với x > 2017