n)\(\dfrac{15}{\sqrt{6}+1}+\dfrac{4}{\sqrt{6}-2}-\dfrac{12}{3-\sqrt{6}}-\sqrt{\dfrac{1}{6}}\)
=\(\dfrac{15\left(\sqrt{6}-1\right)}{\left(\sqrt{6}+1\right)\left(\sqrt{6}-1\right)}+\dfrac{4\left(\sqrt{6}+2\right)}{\left(\sqrt{6}-2\right)\left(\sqrt{6}+2\right)}-\dfrac{12\left(3+\sqrt{6}\right)}{\left(3-\sqrt{6}\right)\left(3+\sqrt{6}\right)}-\sqrt{\dfrac{1}{6}}\)
=\(\dfrac{15\left(\sqrt{6}-1\right)}{5}+\dfrac{4\left(\sqrt{6}+2\right)}{2}-\dfrac{12\left(3+\sqrt{6}\right)}{3}-\sqrt{\dfrac{1}{6}}\)
=\(3\left(\sqrt{6}-1\right)+2\left(\sqrt{6}+2\right)-4\left(3+\sqrt{6}\right)-\sqrt{\dfrac{1}{6}}\)
=\(3\sqrt{6}-3+2\sqrt{6}+4-12-4\sqrt{6}-\sqrt{\dfrac{1}{6}}\)
=\(\sqrt{6}-11-\sqrt{\dfrac{1}{6}}\)
=\(\dfrac{5-11\sqrt{6}}{\sqrt{6}}\)
h)\(\sqrt{\left(\sqrt{3}-3\right)^2}+\sqrt{4-2\sqrt{3}}\)
=\(\left|\sqrt{3}-3\right|+\sqrt{3-2\sqrt{3}+1}\)
=\(3-\sqrt{3}+\sqrt{\left(\sqrt{3}-1\right)^2}\)
=\(3-\sqrt{3}+\left|\sqrt{3}-1\right|\)
=\(3-\sqrt{3}+\sqrt{3}-1\)
=2
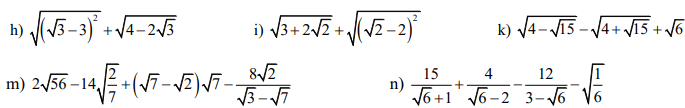
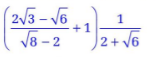
với x ³ 0 và x ¹ 1.
với x > 2017