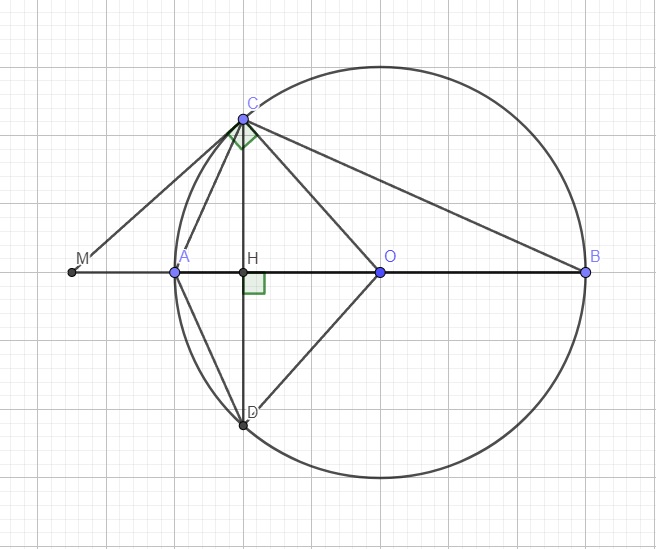
Ta có: \(AB\perp CD\Rightarrow\) H là trung điểm CD (t/c bán kính vuông góc dây cung)
\(\Rightarrow\Delta ACD\) cân tại A (AH đồng thời là trung tuyến và đường cao)
\(\Rightarrow\widehat{ACD}=\widehat{ADC}\)
Mà \(\widehat{ADC}=\widehat{MCA}\) (cùng chắn AC)
\(\Rightarrow\widehat{ACD}=\widehat{MCA}\Rightarrow CA\) là phân giác của \(\widehat{MCD}\)
Áp dụng định lý phân giác trong tam giác MCH:
\(\dfrac{AM}{AH}=\dfrac{CM}{CH}\) (1)
Lại có \(\widehat{ACB}\) là góc nt chắn nửa đường tròn \(\Rightarrow\widehat{ACB}=90^0\)
\(\Rightarrow CB\perp CA\)
\(\Rightarrow CB\) là đường phân giác ngoài góc \(\widehat{MCD}\) của tam giác MCH
Áp dụng định lý phân giác: \(\dfrac{BM}{BH}=\dfrac{CM}{CH}\) (2)
(1);(2) \(\Rightarrow\dfrac{AM}{AH}=\dfrac{BM}{BH}\Rightarrow BM.AH=BH.AM\)