Bài 3: Liên hệ giữa dây và khoảng cách từ tâm tới dây

1. Bài toán

Cho \(AB\) và \(CD\) là hai dây khác đường kính của đường tròn \(\left(O;R\right)\). Gọi \(OH,OK\) lần lượt là khoảng cách từ \(O\) đến \(AB,CD\). Chứng minh: \(OH^2+HB^2=OK^2+KD^2\)?

Lời giải:

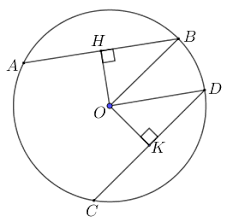
Áp dụng định lí Pytago cho các tam giác vuông \(OHB;OKD\), ta có:

\(\left\{{}\begin{matrix}OH^2+HB^2=OB^2=R^2\\OK^2+KD^2=OD^2=R^2\end{matrix}\right.\)

\(\Rightarrow OH^2+HB^2=OK^2+KD^2\).

Chú ý: Kết luận của bài toán trên vẫn đúng nếu một dây là đường kính hoặc cả 2 dây đều là đường kính.

2. Liên hệ giữa dây và khoảng cách từ tâm đến dây

Trong bài toán ở phần 1, ta có: \(OH^2+HB^2=OK^2+KD^2\quad\left(1\right)\).

Nhớ rằng: Trong một đường tròn, đường kính vuông góc với một dây thì đi qua trung điểm của dây đó.

Do đó, \(H,K\) lần lượt là trung điểm \(AB,CD\). 

Từ đẳng thức (1), ta có: 

• Nếu \(AB=CD\) thì \(BH=DK\) \(\Rightarrow BH^2=KD^2\Rightarrow OH^2=OK^2\Rightarrow OH=OK.\)
• Nếu \(OH=OK\Rightarrow OH^2=OK^2\Rightarrow BH^2=KD^2\Rightarrow BH=DK\), do đó \(AB=CD\).

Ta có kết luận:

Định lí: Trong một đường tròn

• Hai dây bằng nhau thì cách đều tâm.
• Hai dây cách đều tâm thì bằng nhau.

Mặt khác, cũng từ đẳng thức (1), ta có:

• Nếu \(AB>CD\) thì \(BH>DK\) \(\Rightarrow BH^2>DK^2\Rightarrow OH^2< OK^2\Rightarrow OH< OK\).
• Nếu \(OH>OK\) \(\Rightarrow OH^2>OK^2\Rightarrow BH^2< KD^2\Rightarrow BH< KD\), do đó \(AB< CD\).

Ta có kết luận: 

Định lí: Trong một đường tròn

• Dây nào lớn hơn thì dây đó gần tâm hơn.
• Dây nào gần tâm hơn thì dây đó lớn hơn.

Ví dụ: Cho tam giác \(ABC\), \(O\) là giao điểm 3 đường trung trực của tam giác. \(D,E,F\) theo thứ tự là trung điểm \(AB,BC,AC\). Cho biết \(OD>OE,OE=OF\). So sánh các cạnh \(AB,BC,AC\).

Lời giải:

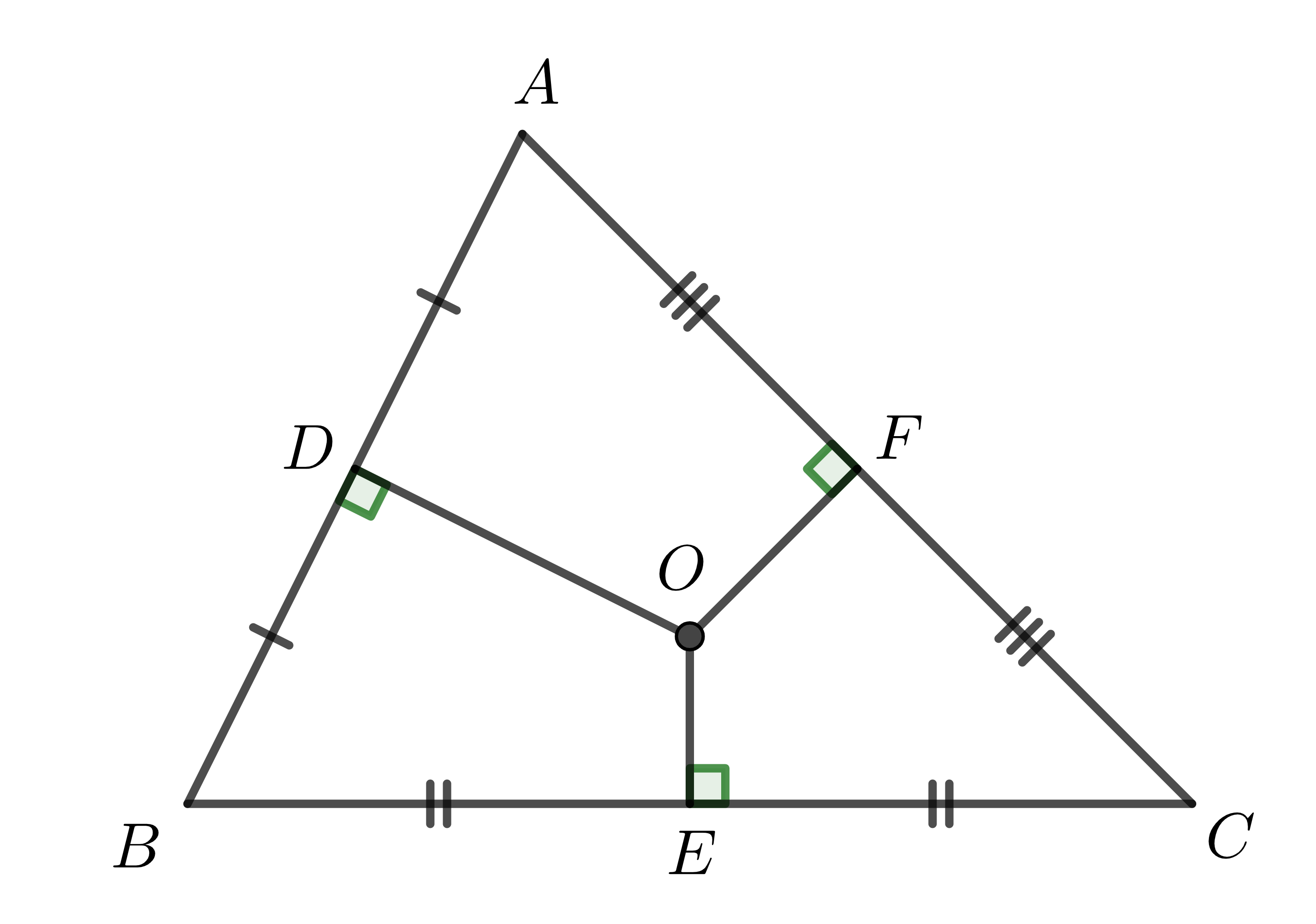
Do \(O\) là giao điểm 3 đường trung trực nên nó là tâm đường tròn ngoại tiếp tam giác \(ABC\).

Xét đường tròn \(\left(O\right)\):

Ta có: \(OD,OE,OF\) theo thứ tự là khoảng cách từ \(O\) đến các dây \(AB,BC,AC\).

\(\left\{{}\begin{matrix}OD>OE\Rightarrow AB< BC\\OE=OF\Rightarrow BC=AC\end{matrix}\right.\) (theo định lí liên hệ giữa dây và khoảng cách từ tâm đến dây)

\(\Rightarrow AB< BC;BC=AC\).