Bài 2: Đường kính và dây của đường tròn

1. So sánh độ dài của đường kính và dây

Định lí 1: Trong các dây của một đường tròn, dây lớn nhất là đường kính.

Thật vậy: Gọi \(AB\) là một dây bất kì của đường tròn \(\left(O;R\right)\). Ta sẽ chứng minh: \(AB\le2R\).

Trường hợp 1: \(AB\) là đường kính \(\Rightarrow AB=2R\).

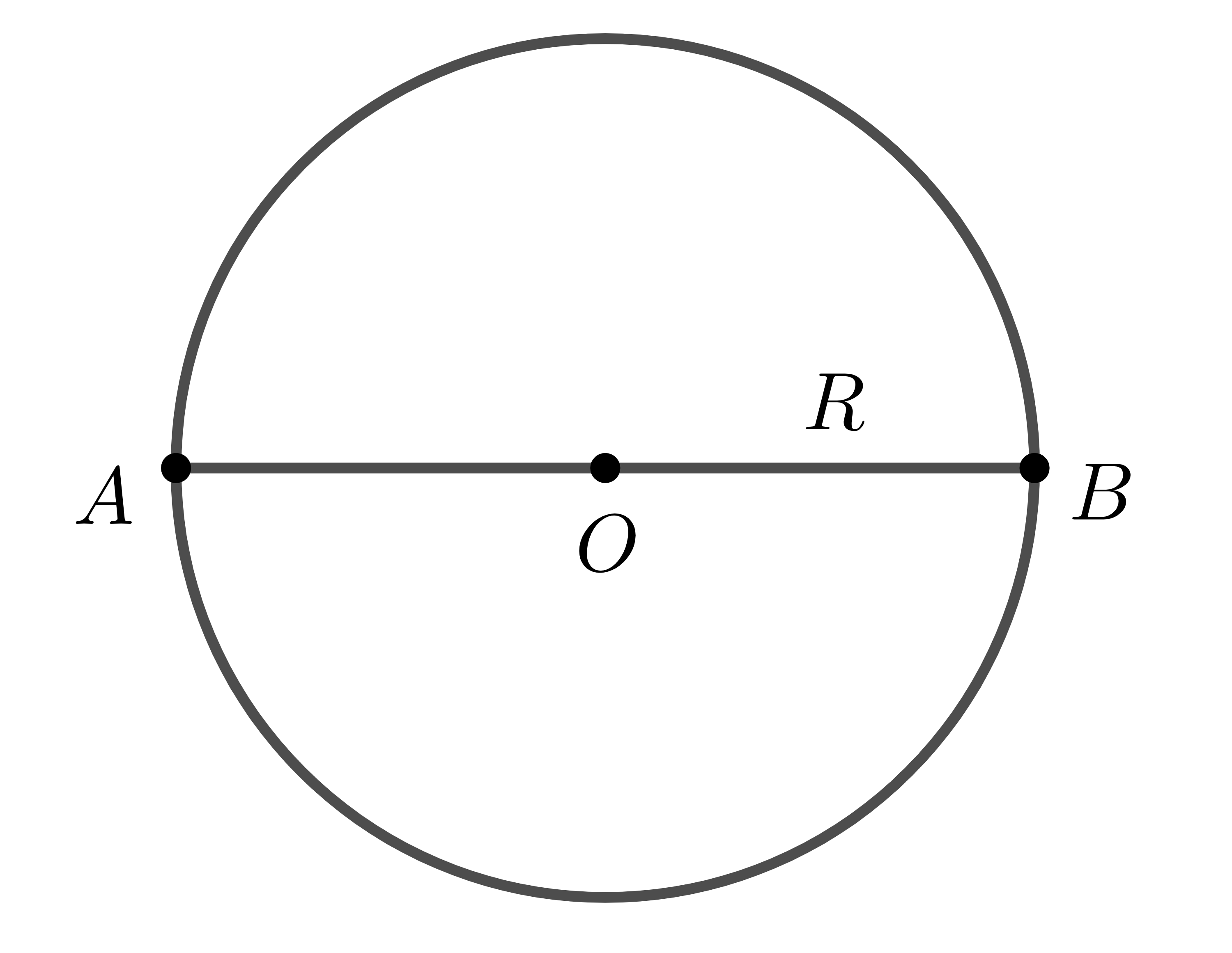
Trường hợp 2: \(AB\) không là đường kính.

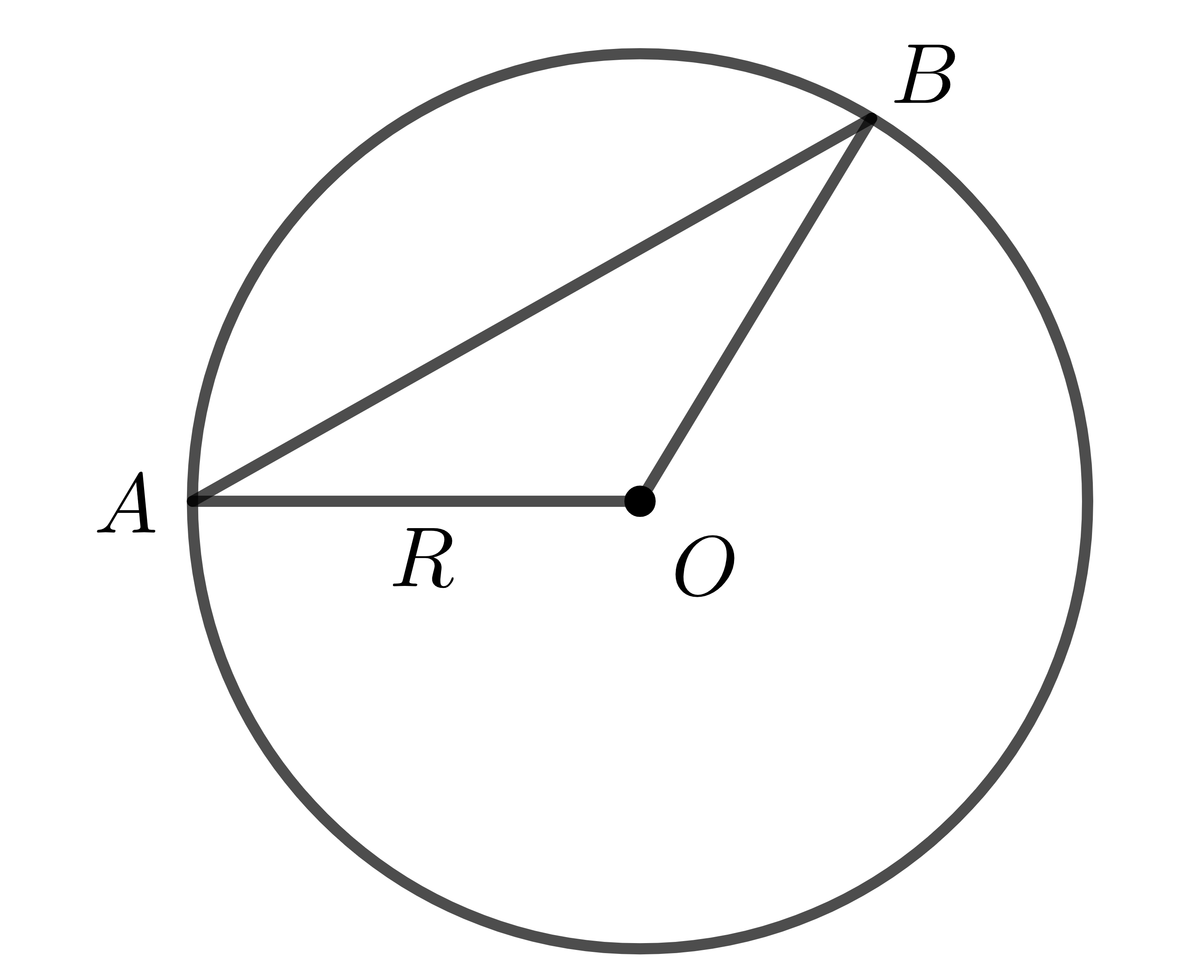
Khi đó, \(OAB\) tạo thành tam giác. Theo bất đẳng thức tam giác ta có: 

\(AB< AO+BO=R+R=2R\).

Vậy, \(AB\le2R\) với mọi dây \(AB\), hay dây lớn nhất trong một đường tròn chính là đường kính của nó.

2. Quan hệ vuông góc giữa đường kính và dây

Định lí 2: Trong một đường tròn, đường kính đi qua trung điểm một dây thì vuông góc với dây ấy.

Chứng minh:

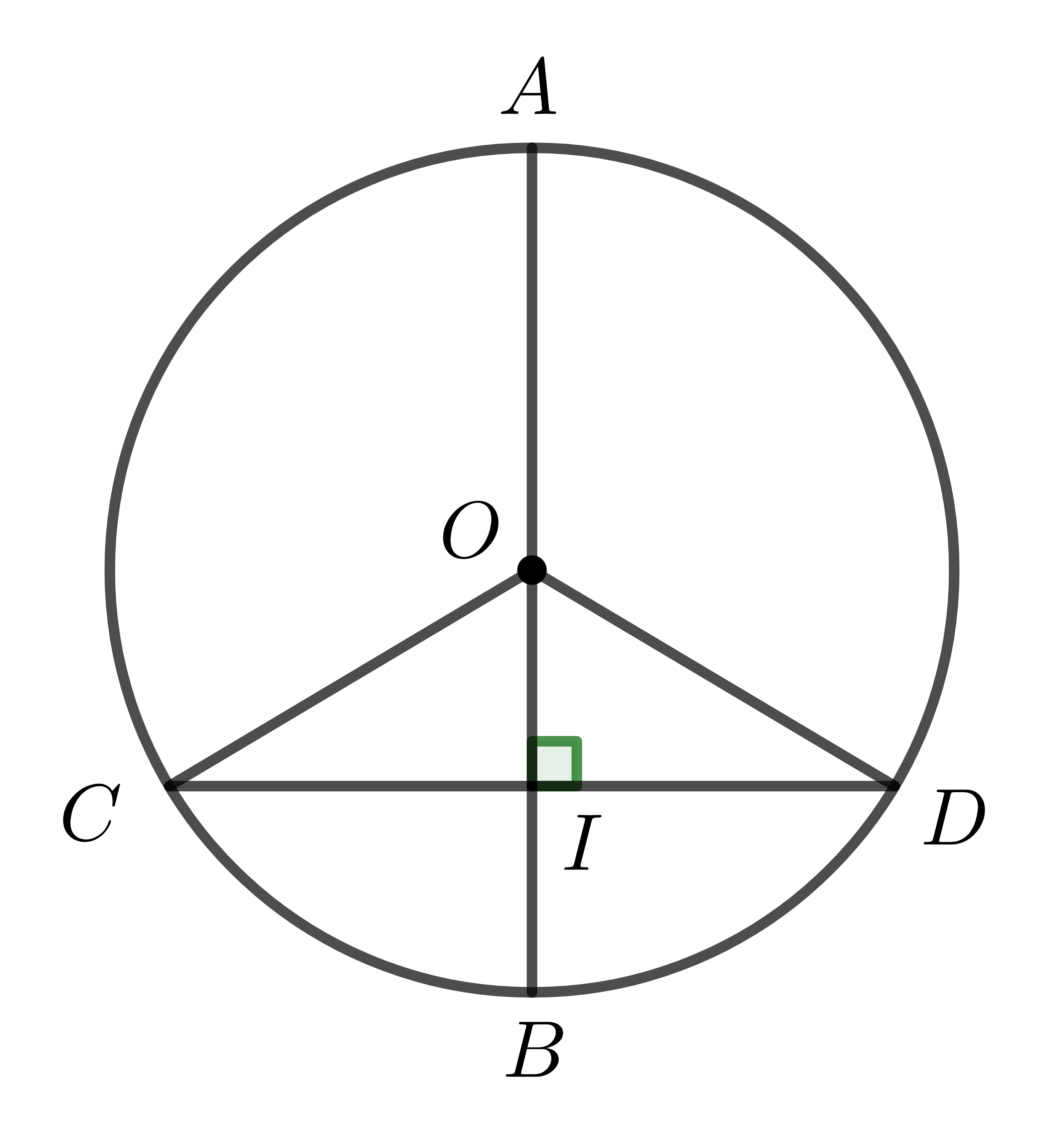
Xét đường tròn \(\left(O\right)\) có đường kính \(AB\) vuông góc với dây \(CD\).

Trường hợp 1: Dây \(CD\) là đường kính. Hiển nhiên đường kính \(AB\) đi qua trung điểm \(O\) của \(CD\).

Trường hợp 2: Dây \(CD\) không là đường kính.

Gọi \(I\) là giao điểm \(AB,CD\).

Tam giác \(OCD\) có \(OC=OD\) nên nó cân tại \(O\) \(\Rightarrow OI\) vừa là đường cao vừa là trung tuyến

\(\Rightarrow I\) là trung điểm \(CD\).

Định lí 3: Trong một đường tròn, đường kính đi qua trung điểm của một dây không đi qua tâm thì vuông góc với dây đó.

Chứng minh:

Cho đường tròn \(\left(O\right)\). Giả sử đường kính \(AB\) cắt dây \(CD\) tại trung điểm \(I\) của nó.

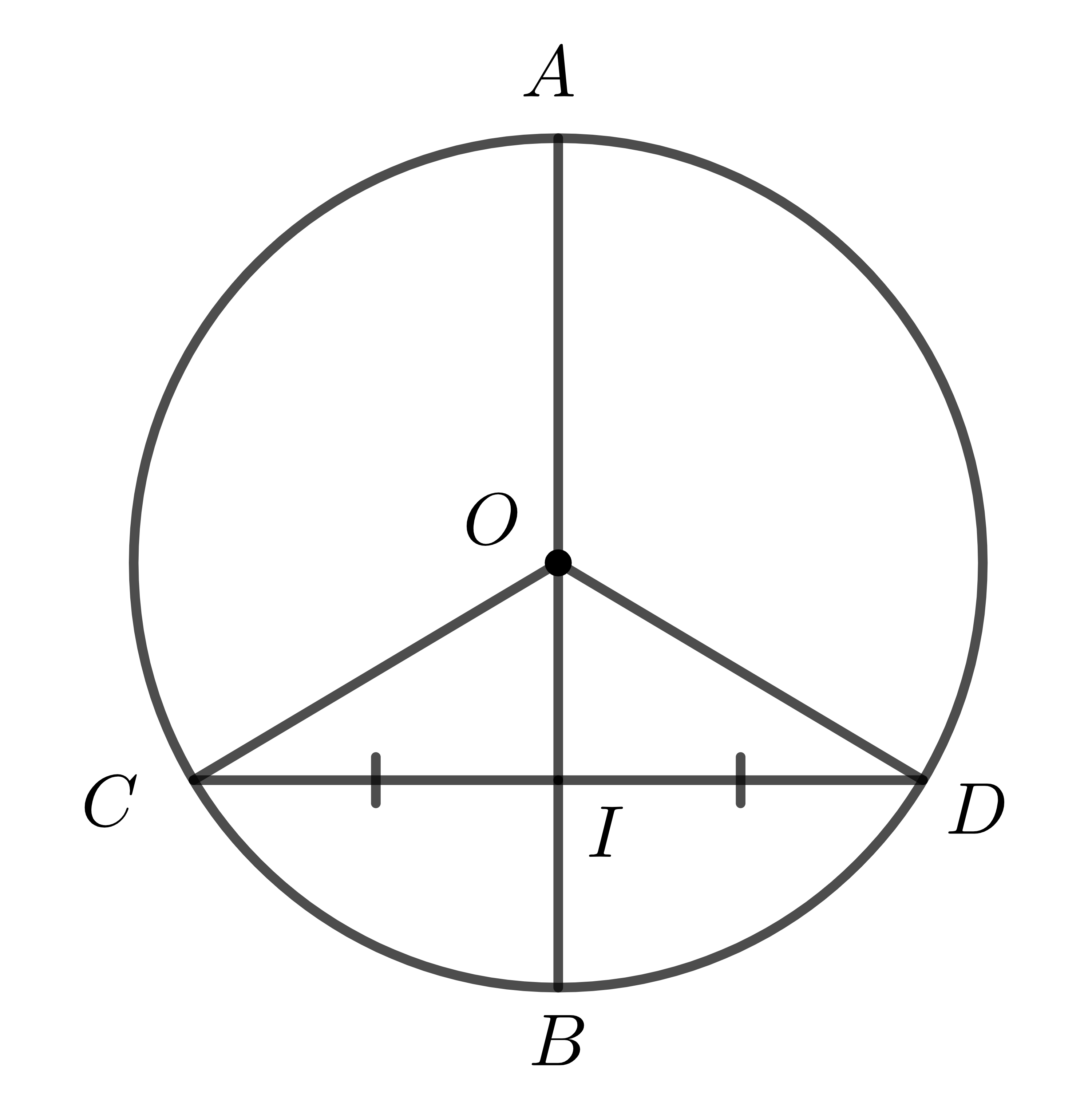
Ta có: \(OI\) chung; \(OC=OD;IC=ID\)

\(\Rightarrow\Delta OIC=\Delta OID\) (cạnh - cạnh - cạnh) \(\Rightarrow\widehat{OIC}=\widehat{OID}=90^0\Rightarrow AB\perp CD\).

Ví dụ: Cho đường tròn \(\left(O;13cm\right)\). Dây \(AB\) không đi qua tâm. Khoảng cách từ \(O\) đến \(AB\) bằng \(5cm\). Tính độ dài dây \(AB\)?

Lời giải: 

Gọi \(M\) là trung điểm \(AB\) \(\Rightarrow MA=MB=\dfrac{AB}{2}\). Theo quan hệ vuông góc giữa đường kính và dây, ta có: \(OM\perp AB\).

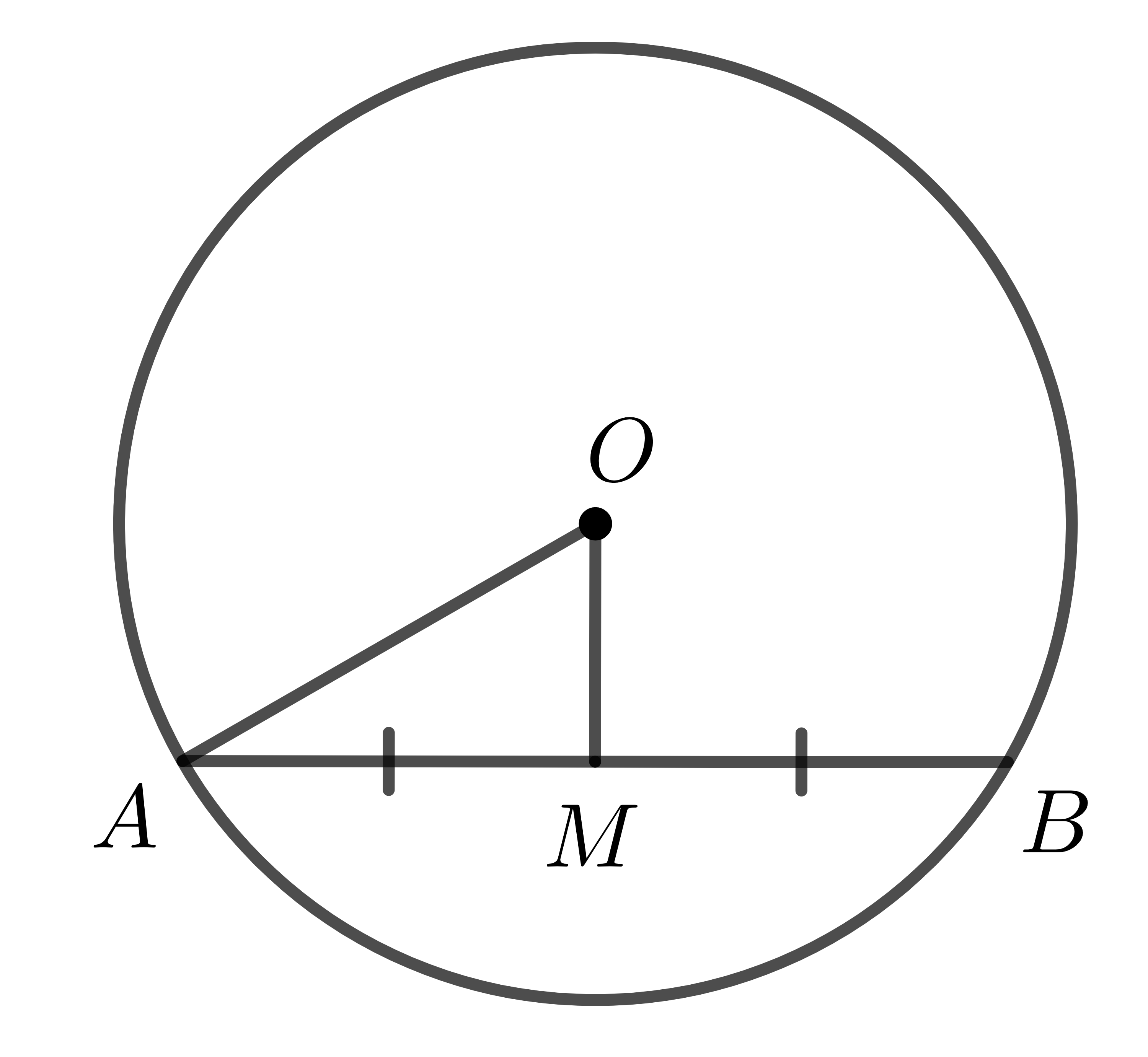
Áp dụng định lí Pytago: \(OA^2=OM^2+MA^2\)

\(\Rightarrow AM=\sqrt{OA^2-OM^2}=\sqrt{13^2-5^2}=12\left(cm\right)\)

\(\Rightarrow AB=2.AM=24\left(cm\right)\).