Bài 4: Vị trí tương đối của đường thẳng và đường tròn
Nội dung lý thuyết
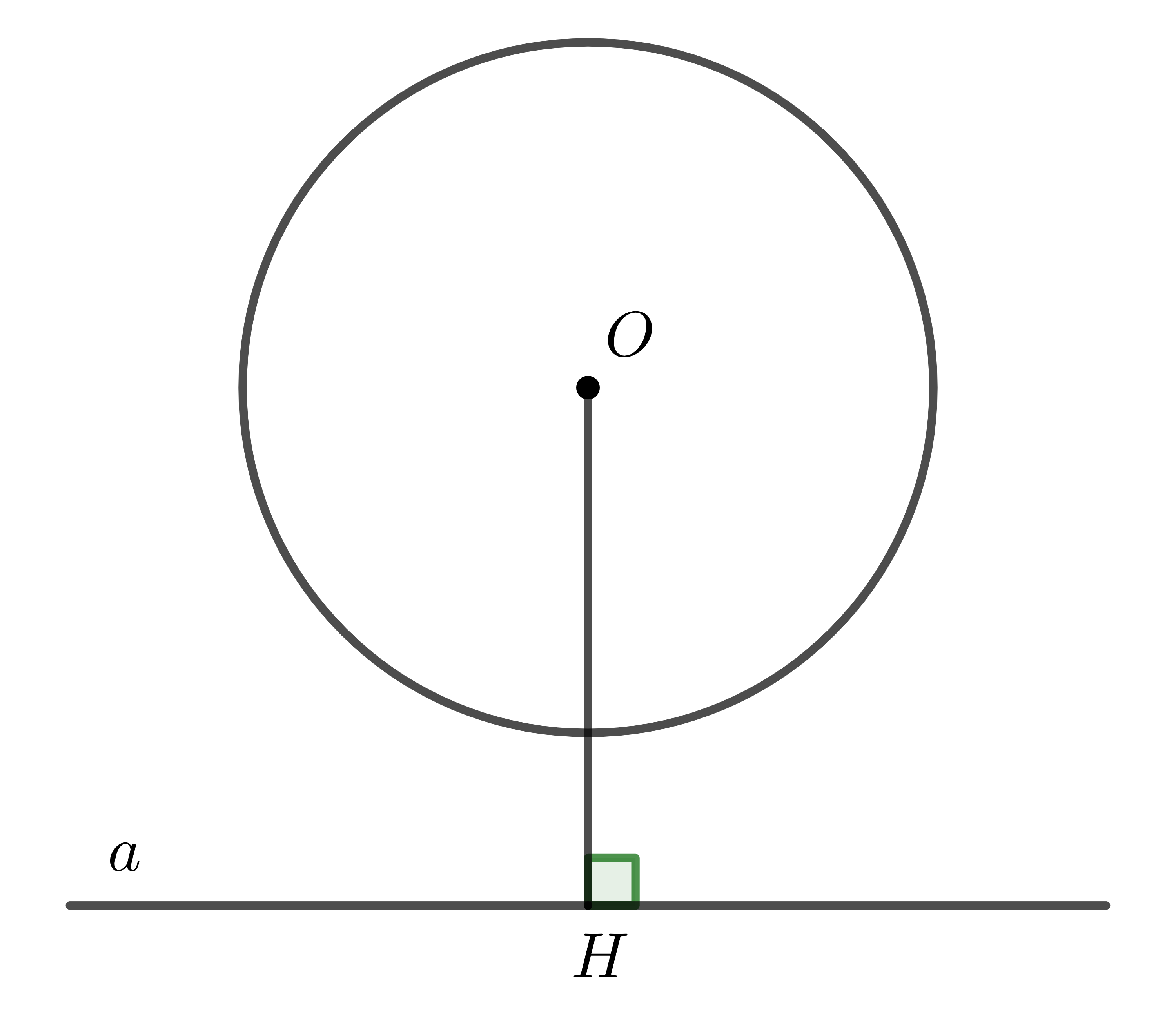
Xét đường tròn \(\left(O;R\right)\) và đường thẳng \(a\). Gọi \(H\) là chân đường vuông góc kẻ từ \(O\) đến đường thẳng \(a\). Khi đó, \(OH\) chính là khoảng cách từ \(O\) đến \(a\). Kí hiệu: \(OH=d\).
1. Ba vị trí tương đối của đường thẳng và đường tròn
Căn cứ vào số điểm chung của đường thẳng và đường tròn, ta có 3 trường hợp:
a) Đường thẳng và đường tròn cắt nhau
Khi đường thẳng \(a\) và đường tròn \(\left(O\right)\) có hai điểm chung \(A,B\) thì ta nói đường thẳng \(a\) và đường tròn \(\left(O\right)\) cắt nhau. Đường thẳng \(a\) được gọi là cát tuyến của đường tròn \(\left(O\right)\).
Khi đó, \(OH=d< R\) và \(HA=HB=\sqrt{R^2-OH^2}\).
Thật vậy:
Nếu đường thẳng \(a\) đi qua \(O\) thì \(OH=d=0\). Khẳng định hiển nhiên đúng.
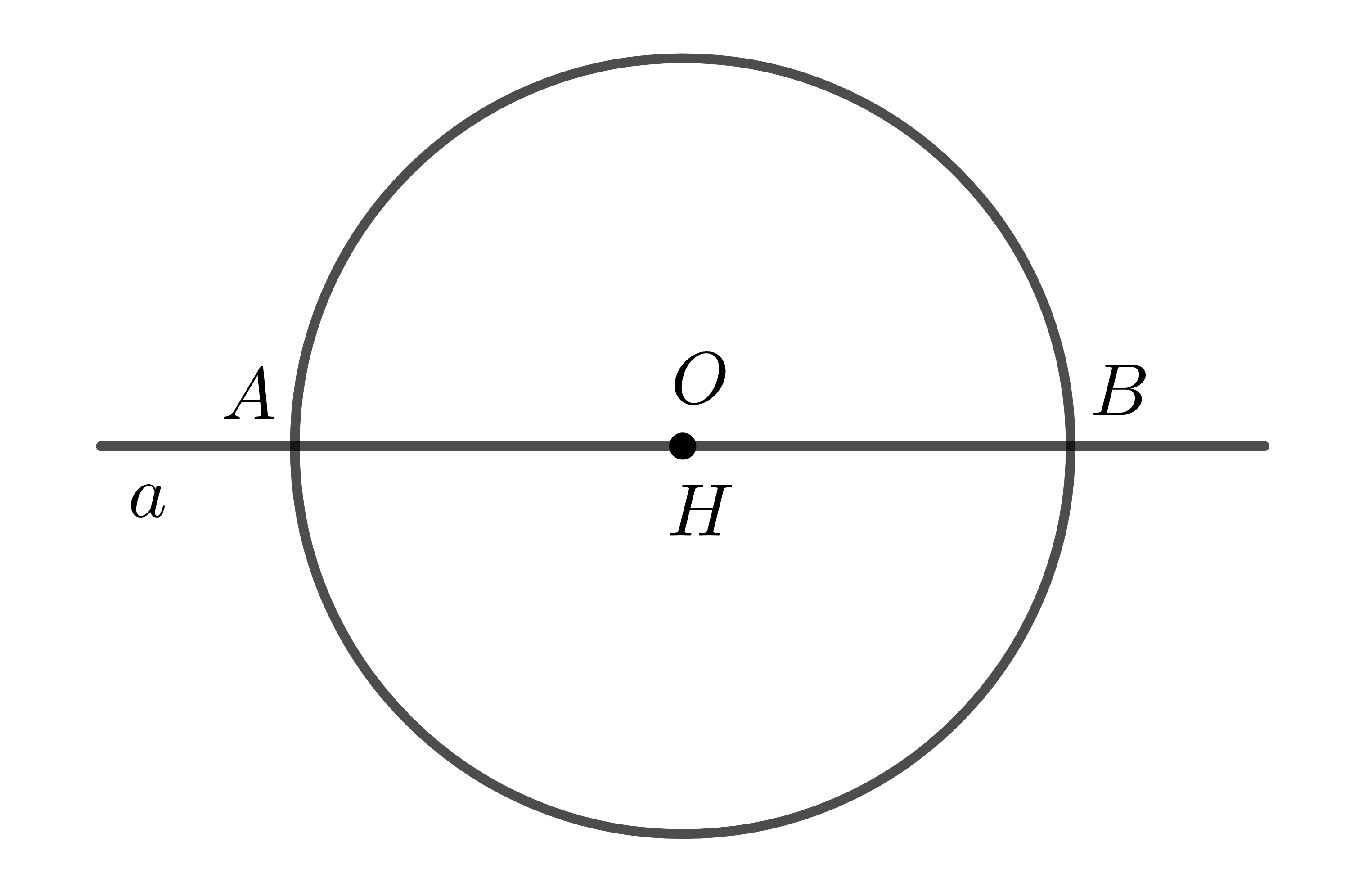
Nếu \(a\) không đi qua \(O\):
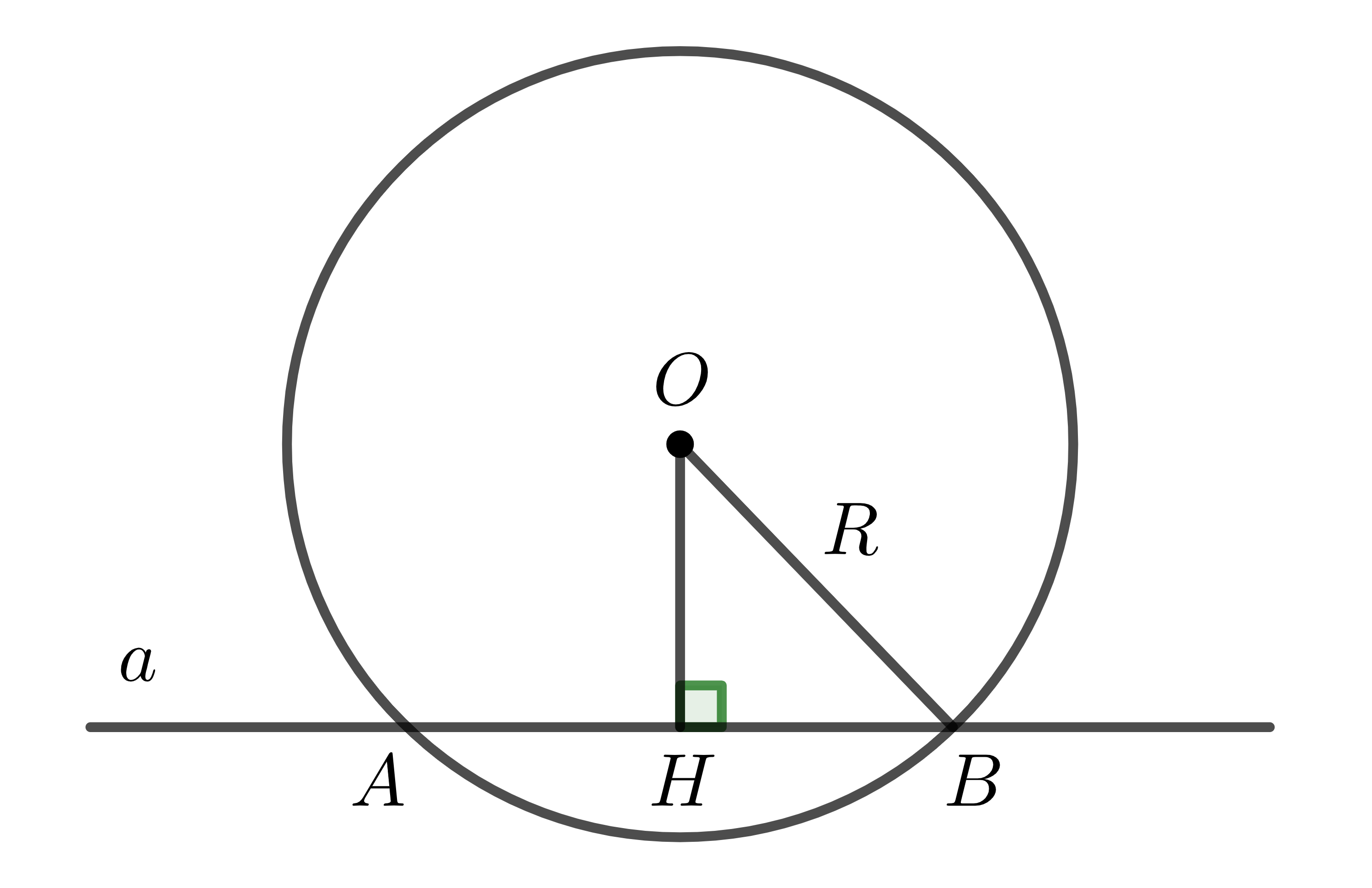
Tam giác \(OHB\) vuông tại \(H\) nên hiển nhiên \(OH=d< R\).
Áp dụng định lí Pytago ta có: \(HB=HA=\sqrt{OB^2-OH^2}=\sqrt{R^2-OH^2}\).
b) Đường thẳng và đường tròn tiếp xúc nhau
Khi đường thẳng \(a\) và đường tròn \(\left(O\right)\) chỉ có một điểm chung \(C\), ta nói đường thẳng \(a\) và đường tròn \(\left(O\right)\) tiếp xúc nhau. Ta nói đường thẳng \(a\) là tiếp tuyến của đường tròn \(\left(O\right)\).
Khi đó \(H\equiv C\), \(OC\perp a\) và \(OH=d=R\).
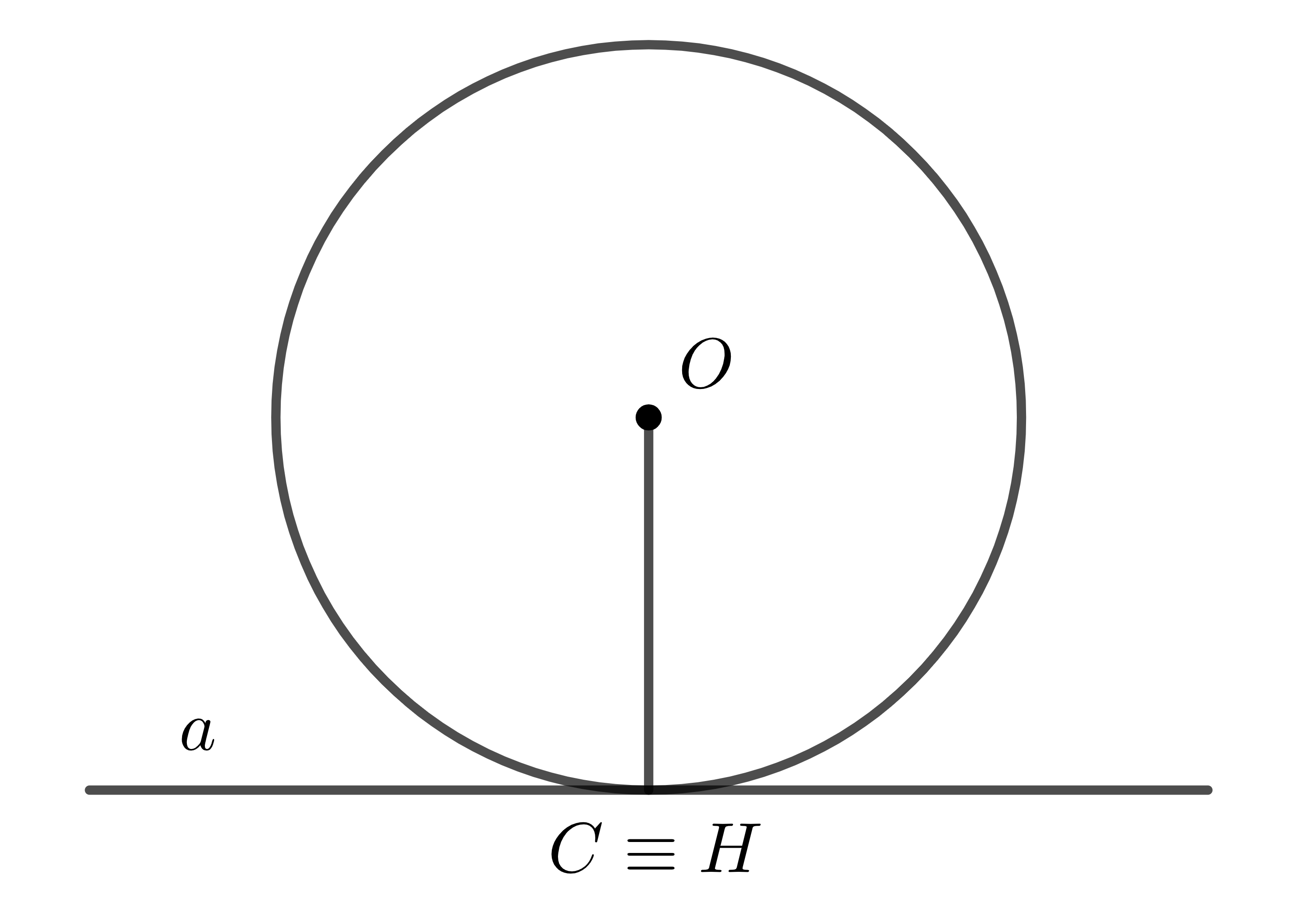
Ta có thể chứng minh khẳng định trên bằng phản chứng: Giả sử \(H\) không trùng \(C\). Lấy \(D\) sao cho \(H\) là trung điểm \(CD\). Khi đó \(C\) không trùng \(D\).
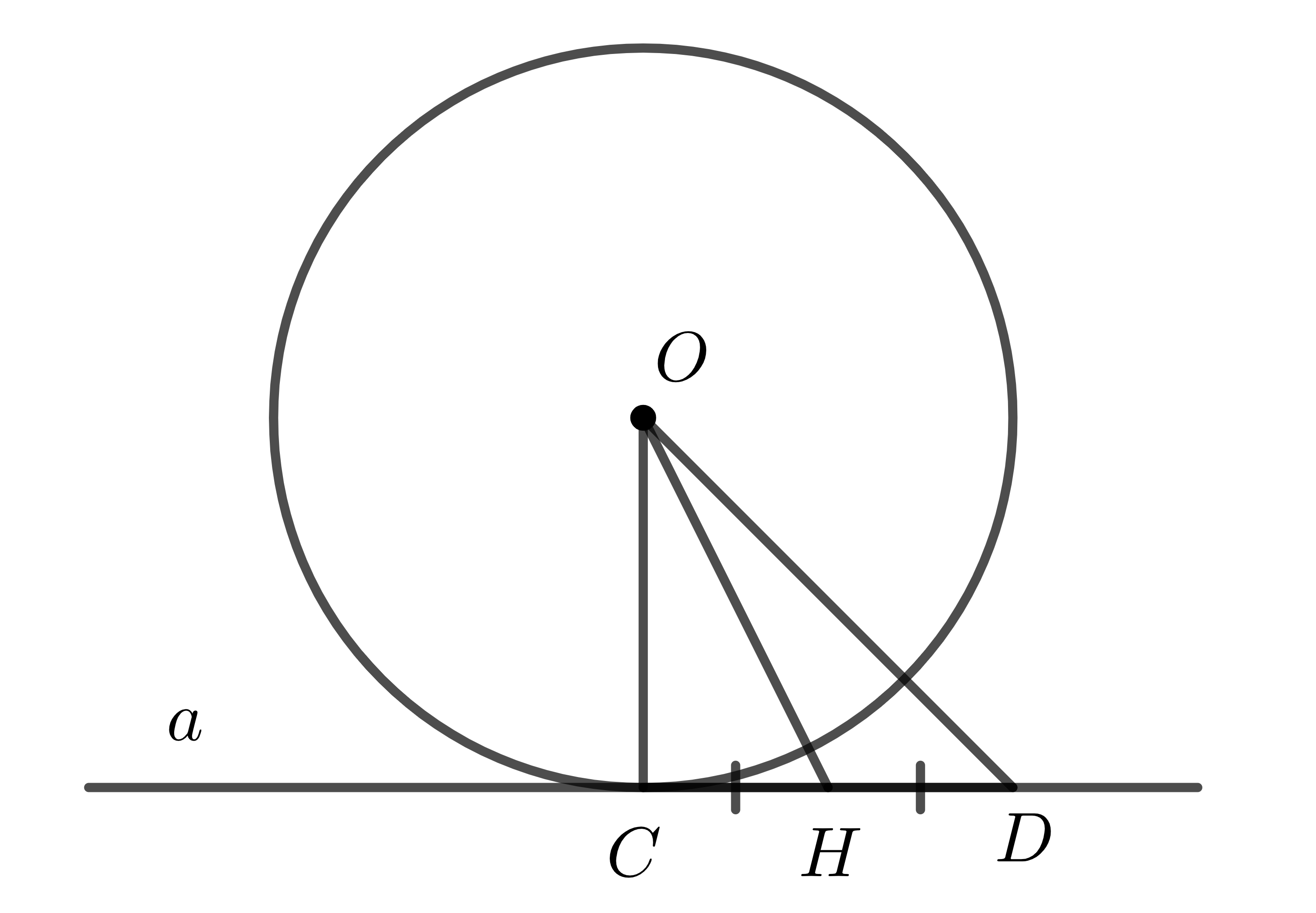
Do \(OH\) là trung trực của \(CD\) nên \(OC=OD=R\) \(\Rightarrow C,D\in\left(O\right)\) (mâu thuẫn giả thiết \(a\) và \(\left(O\right)\) chỉ có một điểm chung).
Vậy \(H\equiv C\), nên \(OC\perp a\) và \(OH=d=R\).
Ta có định lí:
Nếu một đường thẳng là tiếp tuyến của một đường tròn thì nó vuông góc với bán kính đi qua tiếp điểm.
c) Đường thẳng và đường tròn không giao nhau
Khi đường thẳng \(a\) và đường tròn \(\left(O\right)\) không có điểm chung, ta nói đường thẳng \(a\) và đường tròn \(\left(O\right)\) không giao nhau.
Khi đó, \(OH=d>R\).
@56539@@56542@@56547@
2. Hệ thức giữa khoảng cách từ tâm đường tròn đến đường thẳng và bán kính của đường tròn đó
Đặt \(OH=d\), phía trên ta đã thu được kết quả:
- Nếu đường thẳng \(a\) và đường tròn \(\left(O\right)\) cắt nhau thì \(d< R\).
- Nếu đường thẳng \(a\) và đường tròn \(\left(O\right)\) tiếp xúc nhau thì \(d=R\).
- Nếu đường thẳng \(a\) và đường tròn \(\left(O\right)\) không giao nhau thì \(d>R\).
Đảo ngược lại, ta cũng chứng minh được:
- Nếu \(d< R\) thì đường thẳng \(a\) và đường tròn \(\left(O\right)\) cắt nhau.
- Nếu \(d=R\) thì đường thẳng \(a\) và đường tròn \(\left(O\right)\) tiếp xúc nhau.
- Nếu \(d>R\) thì đường thẳng \(a\) và đường tròn \(\left(O\right)\) không giao nhau.
Ta có thể tổng kết các kết luận trong bảng sau:

@347996@@348050@@348143@@348200@