Chương I - Hệ thức lượng trong tam giác vuông
Các câu hỏi tương tự
Cho tam giác ABC vuông tại A có đường cao AH.
Biết AB = 12 cm, AC = 16 cm.
a) Tính độ dài các đoạn thẳng BC, AH,
BH và CH.
b) Kẻ HE ⊥ AB (E ∈ AB) và HF ⊥ AC
(F ∈ AC). Chứng minh rằng AE.AB =
AF.AC và suy ra tam giác ABC ∼ AFE.
Cho tam giác ABC vuông tại A có đường cao AH.
1) Cho biết AB=3 cm, AC=4 cm. Tính độ dài các đoạn BC,HB,HC,AH
2) Vẽ HE vuông góc với AB tại E, HF vuông góc với AC tại F
a) Chứng minh: AE.EB=HE2
b) Chứng minh: AE.EB+AF.FC=AH2
3) Chứng minh: BE=BC. cos3 B
Bài 3: Cho ∆ ABC vuông tại A, đường cao AH biết HB=4cm ; HC= 9cm . a) Tính AB và AH. b) Từ HE vuông góc với AB, HF vuông góc với AC Tử giác AEHF là hình gì? Tính EF ?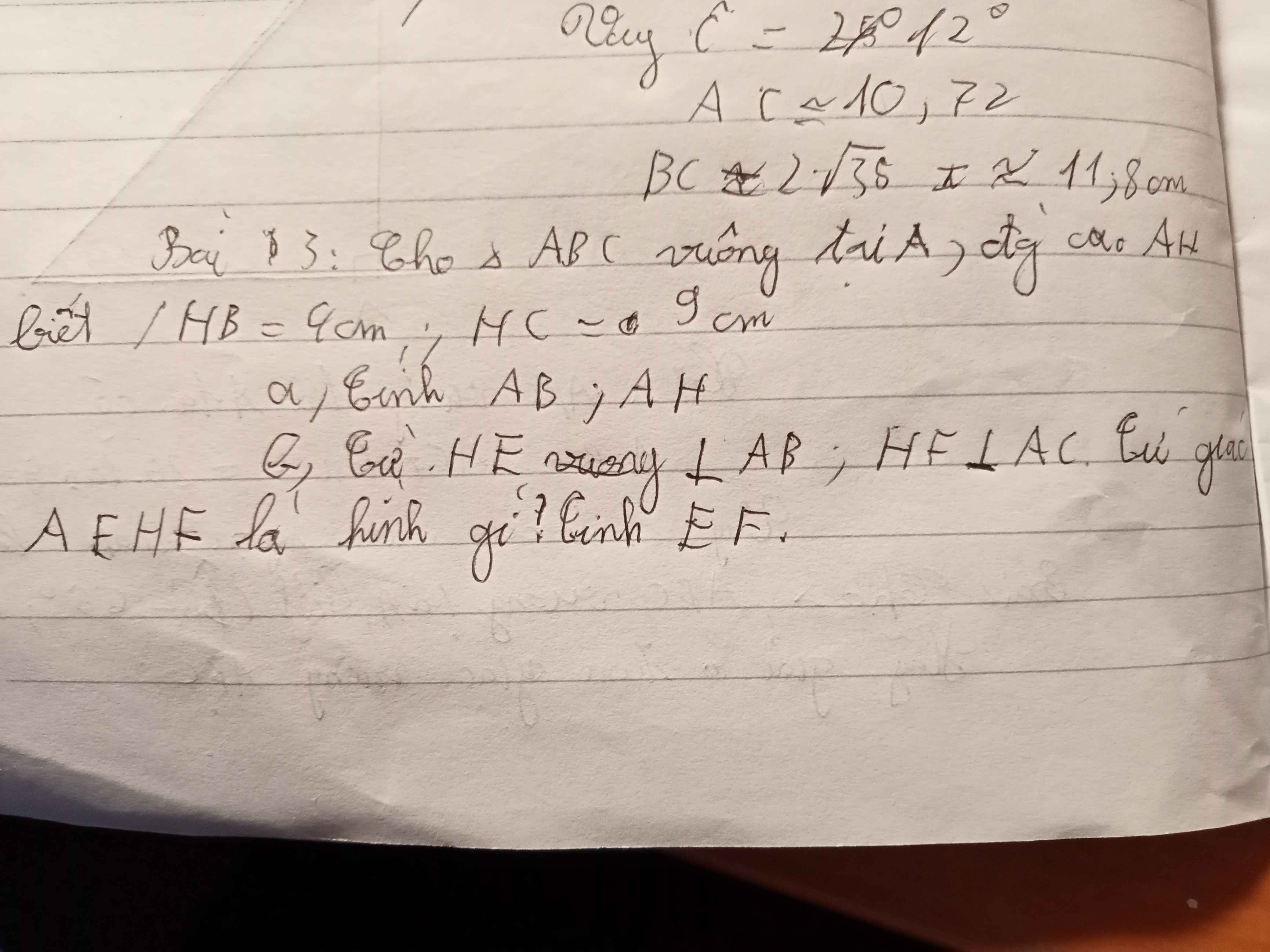
Bài 12: Cho LA BC vuông tại A, đường cao AH . Cho BH = 9cm; H C =16 cm . a/ Tính độ dài AB, AC b/ HE LAB tại E,HF L AC tại F . Chứng minh: A E.A B = AF.A C c/ Lấy điểum K trên cạnh BC, kẻ KM I AB tại M, KN L AC tại N. Chứng minh tam giác HMN vuông.
Cho \(\Delta\)ABC, có AB= 5cm, AC= 12 cm, BC= 13cm.
a, CM ABC vuông.
B, kẻ đường cao AH .Tính AH, BH, CH.
c, Kẻ HE vuông góc với AB, HF vuông góc với AC. CM : AE . AB= AF.AC
d, CM góc AEF= góc CAB.
Cho tam giác ABC vuông tại A, đường cao AH (HϵBC)a) Biết AB 12cm, BC 20cm. Tính AC, B, AH (góc làm tròn đến độ)b) Kẻ HE vuông góc AB (EϵAB). Chứng minh: AE.ABAC2-HC2c) Kẻ HF vuông góc AC (FϵAC). Chứng minh: AFAE.tanC
Đọc tiếp
Cho tam giác ABC vuông tại A, đường cao AH (HϵBC)
a) Biết AB = 12cm, BC = 20cm. Tính AC, B, AH (góc làm tròn đến độ)
b) Kẻ HE vuông góc AB (EϵAB). Chứng minh: AE.AB=AC2-HC2
c) Kẻ HF vuông góc AC (FϵAC). Chứng minh: AF=AE.tanC
cho ΔABC: Â=90o, AH⊥BC, BH=4, HC=9.
A. TÍNH AH, AB, AC
b. Cho HE⊥AB, HF⊥AC. CM: AE.AB=AF.AC
c. BI⊥BC={B} , CẮT AC={K}. CM: BH.BC=AK.AC
d. CM: BE/CF = AB^3/AC^3
e. EF^3 = BE.CF.BC
f. AH^2/AC^2 = BH/BC
Cho tam giác ABC có đường cao AH , biết AH = 4 cm , BH/HC = 1/4 . Tính các cạnh AB , AC , BC , BH , HC
6. Cho tam giác ABC vuông ở A đường cao AH, biết AB = 6cm, AC =8cm. a/ Tính AH; b/ Tính góc HAC; c/ Từ H kẻ HE AB, HF AC. Tính EF










