a/ \(2^{24}=\left(2^2\right)^{12}=4^{12}\)
\(3^{36}=\left(3^3\right)^{12}=27^{12}\)
Vì \(4^{12}< 27^{12}\Leftrightarrow2^{24}< 3^{36}\)
b/ Ta có :
\(2^{332}< 2^{333}=\left(2^3\right)^{111}=8^{111}\)
\(3^{223}>3^{222}=\left(3^2\right)^{111}=9^{111}\)
Vì \(8^{111}< 9^{111}\Leftrightarrow2^{332}< 8^{111}< 9^{111}< 3^{223}\)
\(\Leftrightarrow2^{332}< 3^{223}\)
a)Ta có:
\(2^{24}=\left(2^2\right)^{12}=4^{12}\)
\(3^{36}=\left(3^3\right)^{12}=9^{12}\)
Vì 9>4 nên 9^12>4^12
<=>2^24<3^36
b)Ta có:
\(2^{332}< 2^{333}=\left(2^3\right)^{111}=8^{111}\)
\(3^{223}>3^{222}=\left(3^2\right)^{111}=9^{111}\)
Vì 8^111<9^111 nên 2^332<8^111<9^111<3^223<=>2^332<3^223
a) 224=23.8=88
336=33.12=912
88<98 mà 98<912 =>88<912=>224<336
a.\(2^{24}\) và \(3^{36}\)
\(3^{36}=\left(3^{12}\right)^3\)
\(2^{24}=\left(2^{12}\right)^2\)
Vì \(2^{12}< 3^{13}\Rightarrow2^{24}< 3^{36}\)
Vậy...
b. \(2^{332}\) và \(3^{223}\)
\(2^{332}< 2^{333}\) mà \(2^{333}=\left(2^3\right)^{111}=8^{111}\)
\(3^{223}>3^{222}\) mà \(3^{222}=\left(3^2\right)^{111}=9^{111}\)
Vì \(8^{111}< 9^{111}\Rightarrow2^{332}< 3^{223}\)
Vậy...
b) 2332<2333=23.111=8111
3223>3222=32.111=9111
Ta có 8111<9111=>2333<3222=>2332<3222(mà 3222<3223)=>2332<3223















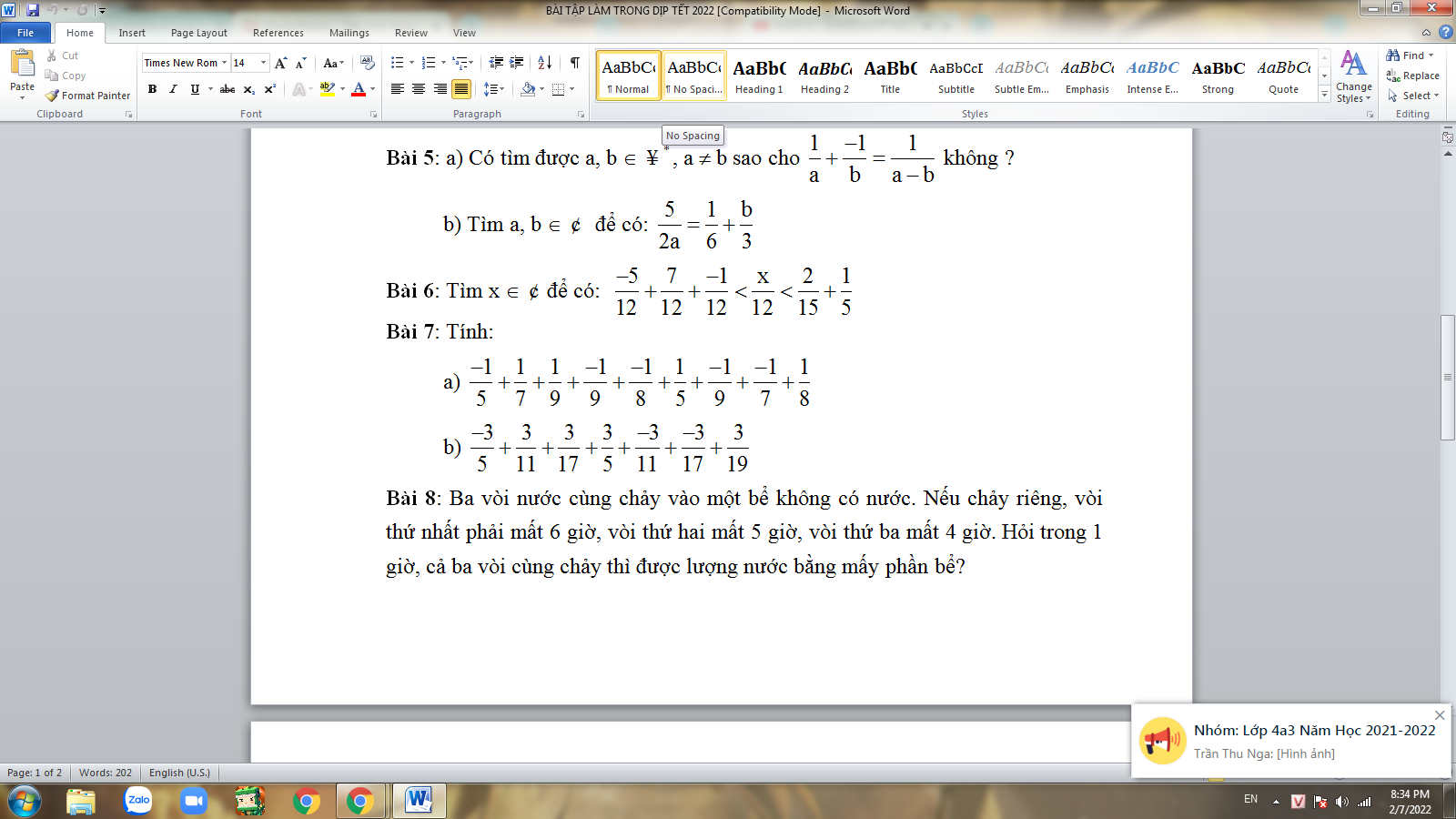 Giúp mình bài 7 và 8
Giúp mình bài 7 và 8