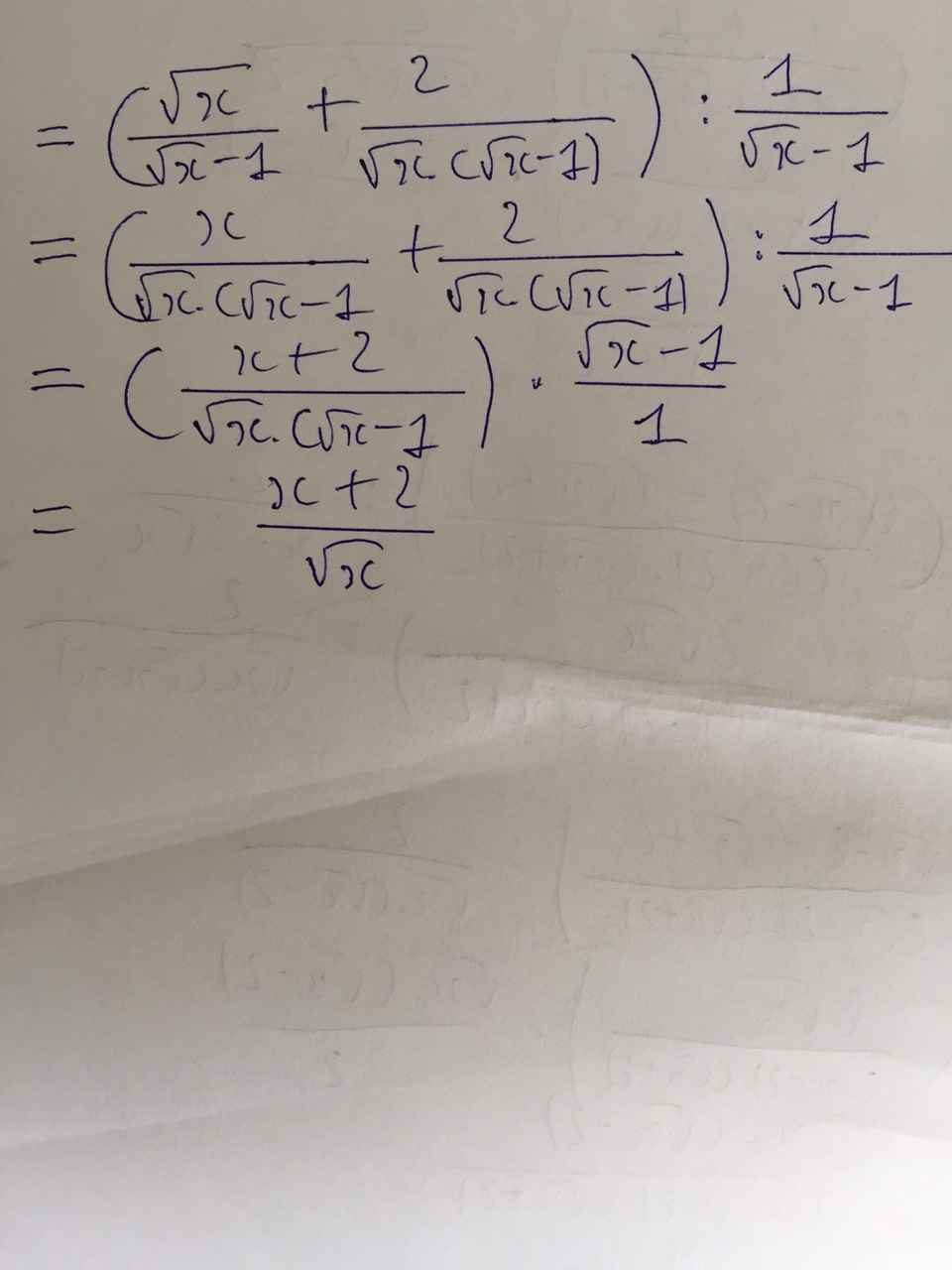(\left(\dfrac{\sqrt{x}}{\sqrt{x}-1}+\dfrac{2}{x-\sqrt{x}}\right):\dfrac{1}{\sqrt{x}-1}\)
`=(x+2)/(x-\sqrtx).(\sqrtx-1)`
`=(x+2)/\sqrtx`
Ôn thi vào 10
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
Rút gọn các biểu thức sau:
a. A = \(\dfrac{1}{2-\sqrt{3}}+\dfrac{1}{2+\sqrt{3}}\)
b. B = \(\left(\dfrac{1}{x-\sqrt{x}}+\dfrac{1}{\sqrt{x}-1}\right):\dfrac{\sqrt{x}+1}{\left(\sqrt{x}-1\right)^2}\) (x > 0 ; x ≠ 1)
Rút gọn các biểu thức sau:
a. \(A=\dfrac{1}{2-\sqrt{3}}+\dfrac{1}{2+\sqrt{3}}\)
b. \(B=\left(\dfrac{1}{x-\sqrt{x}}+\dfrac{1}{\sqrt{x}-1}\right):\dfrac{\sqrt{x}+1}{\left(\sqrt{x}-1\right)^2}\) (x > 0 ; x ≠ 1)
Rút gọn:
\(\dfrac{\sqrt{x}}{\sqrt{x}-1}-\dfrac{6\sqrt{x}-3}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+2\right)}\)
Rút gọn P=\(\left(\dfrac{x-2}{x+2\sqrt{x}}+\dfrac{1}{\sqrt{x}+2}\right)\dfrac{\sqrt{x}+1}{\sqrt{x}-1}\)
Rút gọn P=\(\left(\dfrac{1}{\sqrt{x}-1}+\dfrac{\sqrt{x}}{x-1}\right):\dfrac{2\sqrt{x}+1}{\sqrt{x}-1}\)
P=\(\left(2-\dfrac{2}{1-\sqrt{x}}\right):\left(\dfrac{x+2}{x+\sqrt{x}-2}-\dfrac{\sqrt{x}}{\sqrt{x}=2}\right)\)
rút gọn
\(\dfrac{\sqrt{x}}{\sqrt{x}-1}-\dfrac{6\sqrt{x}-3}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+2\right)}\)
Rút gọn ạ
Rút gọn biểu thức sau:
A = \(\left(\dfrac{\sqrt{x}+2}{\sqrt{x}+1}-\dfrac{2\sqrt{x}-2}{\sqrt{x}-1}\right)\) . \(\left(\sqrt{x}-1\right)\)
1.P= \(\left(\dfrac{\sqrt{x}+1}{\sqrt{2x}-1}+\dfrac{\sqrt{2x}+\sqrt{x}}{\sqrt{2x}-1}-1\right)\):\(\left(1+\dfrac{\sqrt{x}+1}{\sqrt{2x}+1}\dfrac{\sqrt{2x}+\sqrt{x}}{\sqrt{2x}-1}\right)\)
a) Rút gọn P
b) Tính giá trị của P khi x=\(\dfrac{1}{2}\)\(\left(3+2\sqrt{2}\right)\)