Với `x >= 0,x \ne 4` có:
`1/[\sqrt{x}+2]+\sqrt{x}/[2-\sqrt{x}]+[2x-\sqrt{x}+2]/[x-4]`
`=[\sqrt{x}-2-\sqrt{x}(\sqrt{x}+2)+2x-\sqrt{x}+2]/[(\sqrt{x}-2)(\sqrt{x}+2)]`
`=[\sqrt{x}-2-x-2\sqrt{x}+2x-\sqrt{x}+2]/[(\sqrt{x}-2)(\sqrt{x}+2)]`
`=[x-2\sqrt{x}]/[(\sqrt{x}-2)(\sqrt{x}+2)]`
`=[\sqrt{x}(\sqrt{x}-2)]/[(\sqrt{x}-2)(\sqrt{x}+2)]=\sqrt{x}/[\sqrt{x}+2]`
Đúng 2
Bình luận (0)

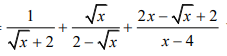



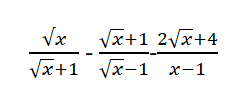
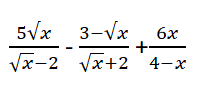


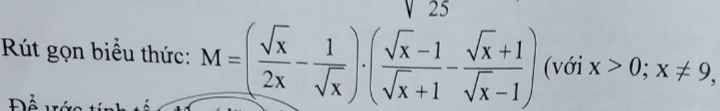



 rút gọn ạ
rút gọn ạ 
