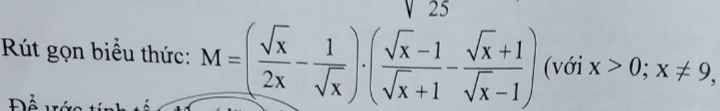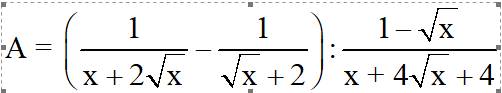\(\dfrac{\sqrt{15}-\sqrt{5}}{\sqrt{3}-1}+\dfrac{5-2\sqrt{5}}{2\sqrt{5}-4}\\ =\dfrac{\sqrt{5}\left(\sqrt{3}-1\right)}{\sqrt{3}-1}+\dfrac{\sqrt{5}\left(\sqrt{5}-2\right)}{2\left(\sqrt{5}-2\right)}\\ =\sqrt{5}+\dfrac{\sqrt{5}}{2}\\ =\dfrac{2\sqrt{5}}{2}+\dfrac{\sqrt{5}}{2}\\ =\dfrac{2\sqrt{5}+\sqrt{5}}{2}\\ =\dfrac{3\sqrt{5}}{2}\)
\(=\dfrac{\sqrt{5}\left(\sqrt{3}-1\right)}{\sqrt{3}-1}+\dfrac{\sqrt{5}\left(\sqrt{5}-2\right)}{2\left(\sqrt{5}-2\right)}\)
=căn 5+1/2*căn 5
=3/2*căn 5
= \(\dfrac{\sqrt{3}.\sqrt{5}-\sqrt{5}}{\sqrt{3}-1}\) + \(\dfrac{\sqrt{5}.\sqrt{5}.2\sqrt{5}}{2\left(\sqrt{5}-2\right)}\)
= \(\dfrac{\sqrt{5}.\left(\sqrt{3}-1\right)}{\sqrt{3}-1}\) +\(\dfrac{\sqrt{5}.\left(\sqrt{5}-2\right)}{2\left(\sqrt{5}-2\right)}\)
=\(\sqrt{5}\) +\(\dfrac{15}{2}\)
=\(\sqrt{5}\left(1+\dfrac{1}{2}\right)\)
= \(\dfrac{3}{2}\) .\(\sqrt{5}\)
=\(\dfrac{3\sqrt{5}}{2}\)








 rút gọn ạ
rút gọn ạ