\(\dfrac{\sqrt{15}-\sqrt{12}}{\sqrt{5}-2}+\dfrac{6+2\sqrt{6}}{\sqrt{3}+\sqrt{2}}\\ =\dfrac{\sqrt{3}\left(\sqrt{5}-\sqrt{4}\right)}{\sqrt{5}-\sqrt{4}}+\dfrac{\sqrt{2}.\sqrt{6}\left(\sqrt{3}+\sqrt{2}\right)}{\sqrt{3}+\sqrt{2}}\\ =\sqrt{3}+\sqrt{12}\\ =\sqrt{3}+\sqrt{2^2.3}\\ =\sqrt{3}+2\sqrt{3}\\ =3\sqrt{3}\)
\(\dfrac{\sqrt{15}-\sqrt{12}}{\sqrt{5}-2}+\dfrac{6+2\sqrt{6}}{\sqrt{3}+\sqrt{2}}\)
\(=\dfrac{\sqrt{3}\left(\sqrt{5}-\sqrt{4}\right)}{\sqrt{5}-2}+\dfrac{\sqrt{12}\left(\sqrt{3}+\sqrt{2}\right)}{\sqrt{3}+\sqrt{2}}\\ =\sqrt{3}+\sqrt{12}\\ =\sqrt{3}+2\sqrt{3}=3\sqrt{3}\)
7) \(\dfrac{\sqrt{15}-\sqrt{12}}{\sqrt{5}-2}+\dfrac{6+2\sqrt{6}}{\sqrt{3}+\sqrt{2}}\)
\(=\dfrac{\sqrt{5}.\sqrt{3}-2\sqrt{3}}{\sqrt{5}-2}+\dfrac{\sqrt{6}.\sqrt{2}.\sqrt{3}+\sqrt{6}.\sqrt{2}.\sqrt{2}}{\sqrt{3}+\sqrt{2}}\)
\(=\dfrac{\sqrt{3}\left(\sqrt{5}-2\right)}{\sqrt{5}-2}+\dfrac{\sqrt{6}.\sqrt{2}\left(\sqrt{3}+\sqrt{2}\right)}{\sqrt{3}+\sqrt{2}}\)
\(=\sqrt{3}+\sqrt{12}=\sqrt{3}+2\sqrt{3}=3\sqrt{3}\)









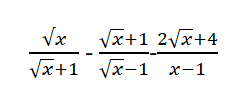
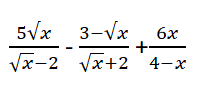

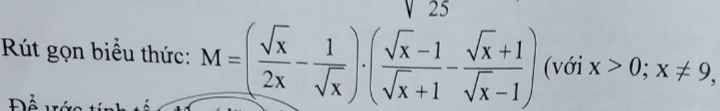



 rút gọn ạ
rút gọn ạ 
