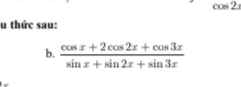\(\left(1-sin^2a\right)cot^2a+1-cot^2a\)
\(=cot^2a-sin^2a.cot^2a+1-cot^2a\)
\(=1-sin^2a.\frac{cos^2a}{sin^2a}=1-cos^2a=sin^2a\)
Đúng 0
Bình luận (0)
Chương 6: CUNG VÀ GÓC LƯỢNG GIÁC. CÔNG THỨC LƯỢNG GIÁC
Các câu hỏi tương tự
Rút gọn: \(\dfrac{sina+cosa-1}{sina-cosa+1}\)
rút gọn
\(\dfrac{sin2a+1}{cos2a}-\dfrac{1-sin2a}{sina-cosb}\)
rút gọn: \(\dfrac{1-2sin^2x}{cos2x-sin2x}\)
Rút gọn biểu thức A= (1+cotx)sin^3x+(1+tanx)cos^3x
Á dụng công thức \(cotx-cot2x=\dfrac{1}{sin2x}\) để rút gọn biểu thức sau
\(S=\dfrac{1}{sina}+\dfrac{1}{sin2a}+\dfrac{1}{sin4a}+\dfrac{1}{sin8a}\)
Cho góc α thỏa mãn sin2α = -4 / 5 và 3π / 4 < α < π. Tính P = sinα - cosα.
19 tháng 4 2021 lúc 15:21
Rút gọn các biểu thức sau
1, \(\dfrac{1+\cot x}{1-\cot x}-\dfrac{2+2\cot^2x}{\left(\tan x-1\right)\left(\tan^2x+1\right)}\)
2, \(\sqrt{\sin^4x+6\cos^2x+3\cos^4x}+\sqrt{\cos^4x+6\sin^2x+3\sin^4x}\)
Áp dụng CT nhân ba \(sin\left(3x\right)=3sinx-4sin^3x\) để rút gọn biểu thức sau:
\(S=\dfrac{1}{3}sin^3a+\dfrac{1}{9}sin^3\left(3a\right)+\dfrac{1}{27}sin^3\left(9a\right)+.....+\dfrac{1}{3^n}sin^3\left(3^{n-1}a\right)\)
Rút gọn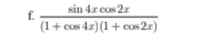 
Rút gọn 