Người ta kéo vật nặng bằng một lực \(\overrightarrow{F}\) có cường độ \(200N\) như hình dưới đây. Khi đó, ta biểu diễn được toạ độ của vector \(\overrightarrow{F}\) trong hệ toạ độ trên là \(\overrightarrow{F}=\left(a\sqrt{2};-b\sqrt{2};c\sqrt{3}\right)\) (với \(a,b,c\in Z\)). Giá trị của biểu thức \(K=a-2b+c\)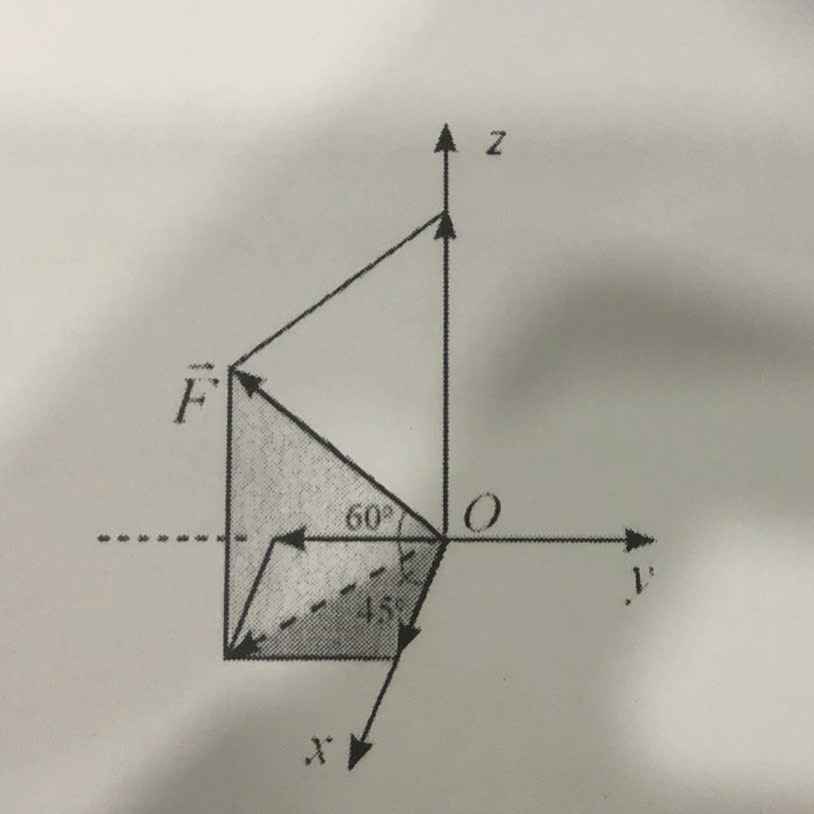
bằng bao nhiêu?
\(F_z=c\sqrt[]{3}=\left|F\right|.sin60^0\Rightarrow c=\dfrac{200.sin60^0}{\sqrt{3}}=100\)
Gọi độ dài hình chiếu của F lên mặt (Oxy) là \(F_{xy}\)
\(\Rightarrow cos60^0=\dfrac{F_{xy}}{\left|F\right|}\Rightarrow F_{xy}=\dfrac{200.1}{2}=100\)
\(F_x=a\sqrt{2}=F_{xy}.cos45^0\Rightarrow a=\dfrac{200.cos45^0}{\sqrt{2}}=100\)
\(F_y=-b\sqrt{2}=F_{xy}.sin45^0\Rightarrow b=\dfrac{200.sin45^0}{-\sqrt{2}}=-100\)
\(\Rightarrow K=400\)