Tích vô hướng của hai vectơ \(\overrightarrow{u}=\left(1;-2;3\right)\) và \(\overrightarrow{v}=\left(3;4;-5\right)\) là:
A. \(\sqrt{14}.\sqrt{50}\). B. \(-\sqrt{14}.\sqrt{50}\). C. 20. D. -20.
Tích vô hướng của hai vectơ \(\overrightarrow{u}=\left(1;-2;3\right)\) và \(\overrightarrow{v}=\left(3;4;-5\right)\) là:
A. \(\sqrt{14}.\sqrt{50}\). B. \(-\sqrt{14}.\sqrt{50}\). C. 20. D. -20.
Độ dài của vectơ \(\overrightarrow{u}=\left(2;-2;1\right)\) là:
A. 9. B. 3. C. 2. D. 4.
Thảo luận (1)Hướng dẫn giải\(\left| {\overrightarrow u } \right| = \sqrt {{2^2} + {{( - 2)}^2} + {1^2}} = 3\)
Chọn B
(Trả lời bởi Nguyễn Quốc Đạt)
Cho hai vectơ \(\overrightarrow{u}=\left(1;-2;3\right)\) và \(\overrightarrow{v}=\left(3;4;-5\right)\). Hãy chỉ ra tọa độ của một vectơ \(\overrightarrow{w}\) khác \(\overrightarrow{0}\) vuông góc với cả hai vectơ \(\overrightarrow{u}\) và \(\overrightarrow{v}\).
Thảo luận (1)Hướng dẫn giải\(\overrightarrow w = ( - 2.( - 5) - 3.4;3.3 - 1.( - 5);1.4 - ( - 2).3) = ( - 2;14;10)\) vuông góc với cả hai vecto \(\overrightarrow u \) và \(\overrightarrow v \)
(Trả lời bởi Nguyễn Quốc Đạt)
Khoảng cách giữa hai điểm I(1; 4; – 7) và K(6; 4; 5) là:
A. 169. B. 13. C. 26. D. 6,5.
Thảo luận (1)Hướng dẫn giải\(\overrightarrow {IK} = (5;0;12) \Rightarrow IK = \sqrt {{5^2} + {{12}^2}} = 13\)
Chọn B
(Trả lời bởi Nguyễn Quốc Đạt)
Cho tam giác MNP có M(0; 2; 1), N(–1; –2; 3) và P(1; 3; 2). Trọng tâm của tam giác MNP có tọa độ là:
A. (0; 1; 2). B. (0; 3; 6). C. (0; – 3; – 6). D. (0; – 1; – 2).
Thảo luận (1)Hướng dẫn giải
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Gọi M, N lần lượt là trung điểm của các cạnh AA' và CC'. Tính góc giữa hai vectơ \(\overrightarrow{MN}\) và \(\overrightarrow{AD'}\).
Thảo luận (1)Hướng dẫn giải

Đặt \(A \equiv O(0;0;0)\)
Ta có: \(D'(0;a;a)\); \(M(0;0; - \frac{a}{2})\); \(N(a;a; - \frac{a}{2})\)
\(\overrightarrow {MN} = (a;a;0)\);\(\overrightarrow {AD'} = (0;a;a)\)
\(\cos (\overrightarrow {MN} ,\overrightarrow {AD'} ) = \frac{{\overrightarrow {MN} .\overrightarrow {AD'} }}{{\left| {\overrightarrow {MN} } \right|.\left| {\overrightarrow {AD'} } \right|}} = \frac{{a.a}}{{\sqrt {{a^2} + {a^2}} .\sqrt {{a^2} + {a^2}} }} = \frac{{{a^2}}}{{2{a^2}}} = \frac{1}{2} \Rightarrow (\overrightarrow {MN} ,\overrightarrow {AD'} ) = 60^\circ \)
(Trả lời bởi Nguyễn Quốc Đạt)
Trong không gian với hệ toạ độ Oxyz, cho A(2; 0; – 3), B(0; – 4; 5) và C(– 1; 2; 0).
a) Chứng minh rằng ba điểm A, B, C không thẳng hàng.
b) Tìm toạ độ của điểm D sao cho tứ giác ABCD là hình bình hành.
c) Tìm toạ độ trọng tâm G của tam giác ABC.
d) Tính chu vi của tam giác ABC.
e) Tính \(\cos\widehat{BAC}\).
Thảo luận (1)Hướng dẫn giảia) \(\overrightarrow {AB} = ( - 2; - 4;8)\); \(\overrightarrow {AC} = ( - 3;2;3)\)
Ta có: \(\overrightarrow {AB} \ne k\overrightarrow {AC} \) => A, B, C không thẳng hàng
b) Để ABCD là hình bình hành thì \(\overrightarrow {AB} = \overrightarrow {DC} \)
Gọi D(a;b;c) => \(\overrightarrow {DC} = ( - 1 - a;2 - b; - c)\)
\(\overrightarrow {AB} = \overrightarrow {DC} \Leftrightarrow ( - 2;-4;8) = ( - 1 - a;2 - b; - c) \Leftrightarrow a = 2;b = 0;c = - 3 \Rightarrow D(1;6; - 8)\)
c) \(G(\frac{1}{3};\frac{{ - 2}}{3};\frac{2}{3})\)
d) \(\overrightarrow {BC} = ( - 1;6; - 5) \Rightarrow BC = \sqrt {62} \)
\(\overrightarrow {AB} = ( - 2; - 4;8) \Rightarrow AB = 2\sqrt {21} \)
\(\overrightarrow {AC} = ( - 3;2;3) \Rightarrow AC = \sqrt {22} \)
Chu vi của tam giác ABC là: AB + AC + BC = \(2\sqrt {21} \)+\(\sqrt {22} \)+\(\sqrt {62} \)
e) \(\cos \widehat {BAC} = \frac{{\overrightarrow {AB} .\overrightarrow {AC} }}{{\left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AC} } \right|}} = \frac{{ - 2.( - 3) - 4.2 + 8.3}}{{\sqrt {{{( - 2)}^2} + {{( - 4)}^2} + {8^2}} .\sqrt {{{( - 3)}^2} + {2^2} + {3^2}} }} = \frac{{\sqrt {462} }}{{42}}\)
(Trả lời bởi Nguyễn Quốc Đạt)
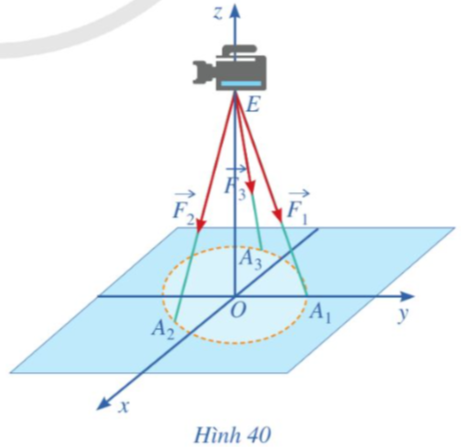
Một chiếc máy được đặt trên một giá đỡ ba chân với điểm đặt E(0 ; 0 ; 6) và các điểm tiếp xúc với mặt đất của ba chân lần lượt là \(A_1\left(0;1;0\right),A_2\left(\dfrac{\sqrt{3}}{2};-\dfrac{1}{2};0\right),A_3=\left(-\dfrac{\sqrt{3}}{2};-\dfrac{1}{2};0\right)\) (Hình 40).
Biết rằng trọng lượng của chiếc máy là 300 N. Tìm tọa độ của các lực tác dụng lên giá đỡ \(\overrightarrow{F_1},\overrightarrow{F_2},\overrightarrow{F_3}\).
Thảo luận (1)Hướng dẫn giảiTa có:
\(\left| {\overrightarrow {{A_1}O} } \right| = \sqrt {{{(0 - 0)}^2} + {{(1 - 0)}^2} + {{(0 - 0)}^2}} = 1\);
\(\left| {\overrightarrow {{A_2}O} } \right| = \sqrt {{{\left( {\frac{{\sqrt 3 }}{2} - 0} \right)}^2} + {{\left( { - \frac{1}{2} - 0} \right)}^2} + {{(0 - 0)}^2}} = 1\);
\(\left| {\overrightarrow {{A_3}O} } \right| = \sqrt {{{\left( { - \frac{{\sqrt 3 }}{2} - 0} \right)}^2} + {{\left( { - \frac{1}{2} - 0} \right)}^2} + {{(0 - 0)}^2}} = 1\).
Do đó \({A_1}O = {A_2}O = {A_3}O = 1\), suy ra O là trọng tâm tam giác \({A_1}{A_2}{A_3}\).
Khi đó \(\overrightarrow {E{A_1}} + \overrightarrow {E{A_2}} + \overrightarrow {E{A_3}} = 3\overrightarrow {EO} \) (tính chất trọng tâm).
Mặt khác, dễ dàng chứng minh độ dài các giá đỡ \(E{A_1} = E{A_2} = E{A_3}\) (do các tam giác vuông \(EO{A_1}\), \(EO{A_2}\), \(EO{A_3}\) bằng nhau). Các lực \(\overrightarrow {{F_1}} \), \(\overrightarrow {{F_2}} \), \(\overrightarrow {{F_3}} \) cùng phương với các giá đỡ và có độ lớn bằng nhau nên ta có tỉ lệ:
\(\frac{{\left| {\overrightarrow {{F_1}} } \right|}}{{E{A_1}}} = \frac{{\left| {\overrightarrow {{F_2}} } \right|}}{{E{A_2}}} = \frac{{\left| {\overrightarrow {{F_3}} } \right|}}{{E{A_3}}} = k\) và \(\overrightarrow {{F_1}} = k\overrightarrow {E{A_1}} \), \(\overrightarrow {{F_2}} = k\overrightarrow {E{A_2}} \), \(\overrightarrow {{F_3}} = k\overrightarrow {E{A_3}} \).
Từ \(\overrightarrow {E{A_1}} + \overrightarrow {E{A_2}} + \overrightarrow {E{A_3}} = 3\overrightarrow {EO} \) đã chứng minh, ta được:
\(k\overrightarrow {E{A_1}} + k\overrightarrow {E{A_2}} + k\overrightarrow {E{A_3}} = 3k\overrightarrow {EO} \)
\( \Leftrightarrow \overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow {{F_3}} = 3k\overrightarrow {EO} \).
Mà \(\overrightarrow {EO} = (0 - 0;0 - 0;0 - 6) = (0;0 - 6)\).
Suy ra \(\overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow {{F_3}} = (0;0; - 18k)\).
Giả sử \(\overrightarrow P \) là trọng lực tác động lên cả 3 giá đỡ. \(\overrightarrow P \) là lực vuông góc với mặt phẳng (Oxy), hướng xuống dưới (ngược chiều với trục Oz) nên tọa độ của \(\overrightarrow P = (0;0; - 300)\).
Suy ra \(\overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow {{F_3}} = \overrightarrow P \Leftrightarrow - 18k = - 300 \Leftrightarrow k = \frac{{50}}{3}\).
Vậy \(\overrightarrow {{F_1}} = (0;\frac{{50}}{3}; - 100)\); \(\overrightarrow {{F_2}} = (\frac{{25\sqrt 3 }}{3}; - \frac{{25}}{3}; - 100)\); \(\overrightarrow {{F_3}} = ( - \frac{{25\sqrt 3 }}{3}; - \frac{{25}}{3}; - 100)\).
(Trả lời bởi Nguyễn Quốc Đạt)
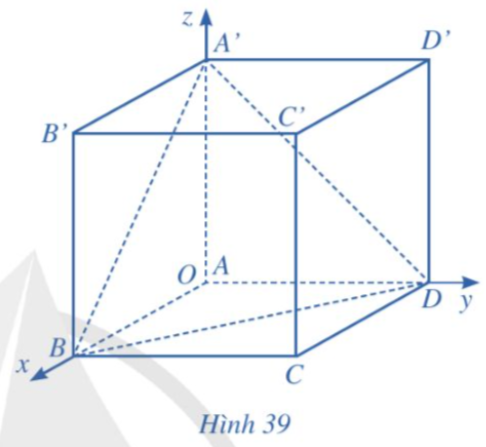
Xét hệ toạ độ Oxyz gắn với hình lập phương ABCD.A'B'C'D' như Hình 39, đơn vị của mỗi trục bằng độ dài cạnh hình lập phương. Biết A(0; 0; 0), B(1; 0; 0), D(0; 1; 0), A'(0; 0; 1).
a) Xác định toạ độ các đỉnh còn lại của hình lập phương ABCD.A'B'C'D'.
b) Xác định toạ độ trọng tâm G của tam giác A'BD.
c) Xác định toạ độ các vectơ \(\overrightarrow{OG}\) và \(\overrightarrow{OC'}\). Chứng minh rằng ba điểm O, G, C' thẳng hàng và OG = \(\dfrac{1}{3}OC'\).
Thảo luận (1)Hướng dẫn giảia) C(1;1;0); B’(1;0;1); C’(1;1;1); D’(0;1;1)
b) \(G(\frac{1}{3};\frac{1}{3};\frac{1}{3})\)
c) \(\overrightarrow {OG} = (\frac{1}{3};\frac{1}{3};\frac{1}{3})\)
\(\overrightarrow {OC'} = (1;1;1)\)
Ta có: \(\overrightarrow {OG} = \frac{1}{3}\overrightarrow {OC'} \) => O, G, C’ thẳng hàng
\(\left| {\overrightarrow {OG} } \right| = \frac{1}{3}\left| {\overrightarrow {OC'} } \right|\;\;hay\;\;OG = \frac{1}{3}OC\)
(Trả lời bởi Nguyễn Quốc Đạt)
Cho hai điểm M(1; – 2; 3) và N(3; 4; – 5). Trung điểm của đoạn thẳng MN có tọa độ là:
A. (– 2; 1; 1). B. (2; 1; 1). C. (– 2; 1; – 1). D. (2; 1; – 1).
Thảo luận (1)Hướng dẫn giải