x-y=0 nên x=y
\(A=xy-xy^2=x^2-x^3\)
\(B=x^2y+y^2-2xy\)
\(=x^3+x^2-2\cdot x\cdot x\)
\(=x^3-x^2=-\left(x^2-x^3\right)\)
=>A và B là hai đa thức đối nhau
x-y=0 nên x=y
\(A=xy-xy^2=x^2-x^3\)
\(B=x^2y+y^2-2xy\)
\(=x^3+x^2-2\cdot x\cdot x\)
\(=x^3-x^2=-\left(x^2-x^3\right)\)
=>A và B là hai đa thức đối nhau
Thu gọn đa thức và tìm bậc
A= x2y + \(\dfrac{\text{1}}{\text{3}}\)xy2 + \(\dfrac{\text{3}}{\text{5}}\)xy2 - 2xy + 3x2y - \(\dfrac{\text{2}}{\text{3}}\)
B= \(\dfrac{\text{9}}{\text{5}}\)xy2z + 2x3y2z + \(\dfrac{\text{1}}{\text{5}}\)xy2z - 2x3y2z - 1
cho đa thức A = 5xy2 + xy - xy - 1/3x2y + 2xy + x2y + xy + 6
a) Thu gọn rồi xác định bậc của đa thức kết quả.
b) Tìm đa thức B sao cho A + B = 0
c) Tìm đa thức C sao cho A + C = -2xy + 1.
Cho đa thức \(A=2xy+\dfrac{1}{2}x^3y^2-xy-\dfrac{1}{2}x^3y^2+y-1\)
a) Thu gọn A. Tìm bậc của đa thức A
b) Tính giá trị biểu thức A tại x = 0,1 và y = -2.
Cho hai đa thức: A=x2y+2xy2-7x2y2+x4 B=5x2y2-2xy2-x2y-3x4-1
b) Tính giá trị lớn nhất của A+B
c) Tìm x,y ∈ Z để tổng A và B có giá trị bằng -3
CMR nếu x+y+1=0 thì giá trị của các đa thức sau là hằng số
a) x3+2xy(x+y)+y3+x2+y2+xy+2
Cho đa thức: A = \(-2xy^2+\dfrac{1}{3}x^3y-x-\dfrac{1}{3}x^3y+xy^2+x-4x^2y\). Thu gọn A và tìm bậc của A
Cho hai đa thức sau: P= -x^3y -xy+x^2+4x^3y+2xy+1
Q= x^3y - 8xy - 5+2x^3y+9x^2+4 - 10x^2
a) Thu gọn đa thức P và Q . Xác định bậc của đa thức P và Q sau khi thu gọn.
b) Tính A=P+Q và B=P-Q
c) Tính giá trị của đa thức A khi x=1 và y=-1
Tìm bậc của các đa thức sau (a là hằng số )
a, 2x - 5xy + 3x2
b, ax2 + 2x2 - 3
c, ax3 + 2xy - 5
d, 4y2 - 3y - 3y4
e, -3x5 - 1/2 x3y - 3/4 xy2 + 3x5 + 2
Xác định bậc, hệ số tự do, hệ số cao nhất, của đa thức
P(x)=
Đáp án: Bậc của đa thức là: Trả lời
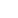
Hệ số tự do của đa thức là: Trả lời
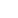
Hệ số cao nhất của đa thức là: