Gọi B là đỉnh ngoạn hải đăng
C và D là 2 vị trí của thuyền
Ta có \(cot\widehat{BDA}=\dfrac{AD}{AB};cot\widehat{BCA}=\dfrac{AC}{AB}\)
\(=>\dfrac{DC}{AB}=\dfrac{DA-CA}{AB}=cot30^o-cot45^o=\sqrt{3}-1\)
\(=>CD=75\left(\sqrt{3}-1\right)\approx54,9m\)
Vậy chiếc thuyền đã chạy đc xấp xỉ 55m sau 2 lần quan sát
- Gọi chiều cao cột hải đăng là \(AB\). Vẽ các góc hạ \(\widehat{ACB}=30^0;\widehat{ADB}=45^0\) (C và D cùng phía so với AB).
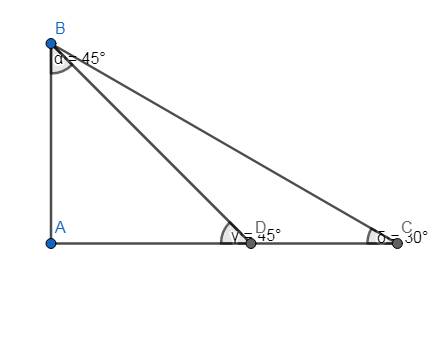
\(\Rightarrow\widehat{ABC}=60^0;\widehat{ABD}=45^0\)
\(\Rightarrow AC>AD\).
\(\Rightarrow D\) nằm giữa A và C.
- \(\Delta ABC\) vuông tại A có: \(AC=\cot30^0.AB=\sqrt{3}.75=75\sqrt{3}\left(cm\right)\).
- \(\Delta ABD\) vuông tại D có: \(AD=\cot45^0.AB=1.75=75\left(cm\right)\)
\(\Rightarrow CD=AC-AD=75\sqrt{3}-75=75\left(-1+\sqrt{3}\right)\left(cm\right)\)














