Gọi số ngày dự kiến là x
THeo đề, ta có: 50x=57(x-1)+13
=>57x-57+13=50x
=>7x=44
=>x=44/7
Vậy: Khối lượng than đội khai thác được là \(57\cdot\left(\dfrac{44}{7}+1\right)+13=\dfrac{2998}{7}\left(m^3\right)\)
Một mảnh đất hình thang vuông XYZK( X=Y=90 độ). Người ta muốn thiết kế một vườn cây cảnh XYMK( M là đường cao YM). Biết XY=12m, KZ=17m, YZ=13m. Tính diện tích phần đất còn lại
Help me!!!!Please
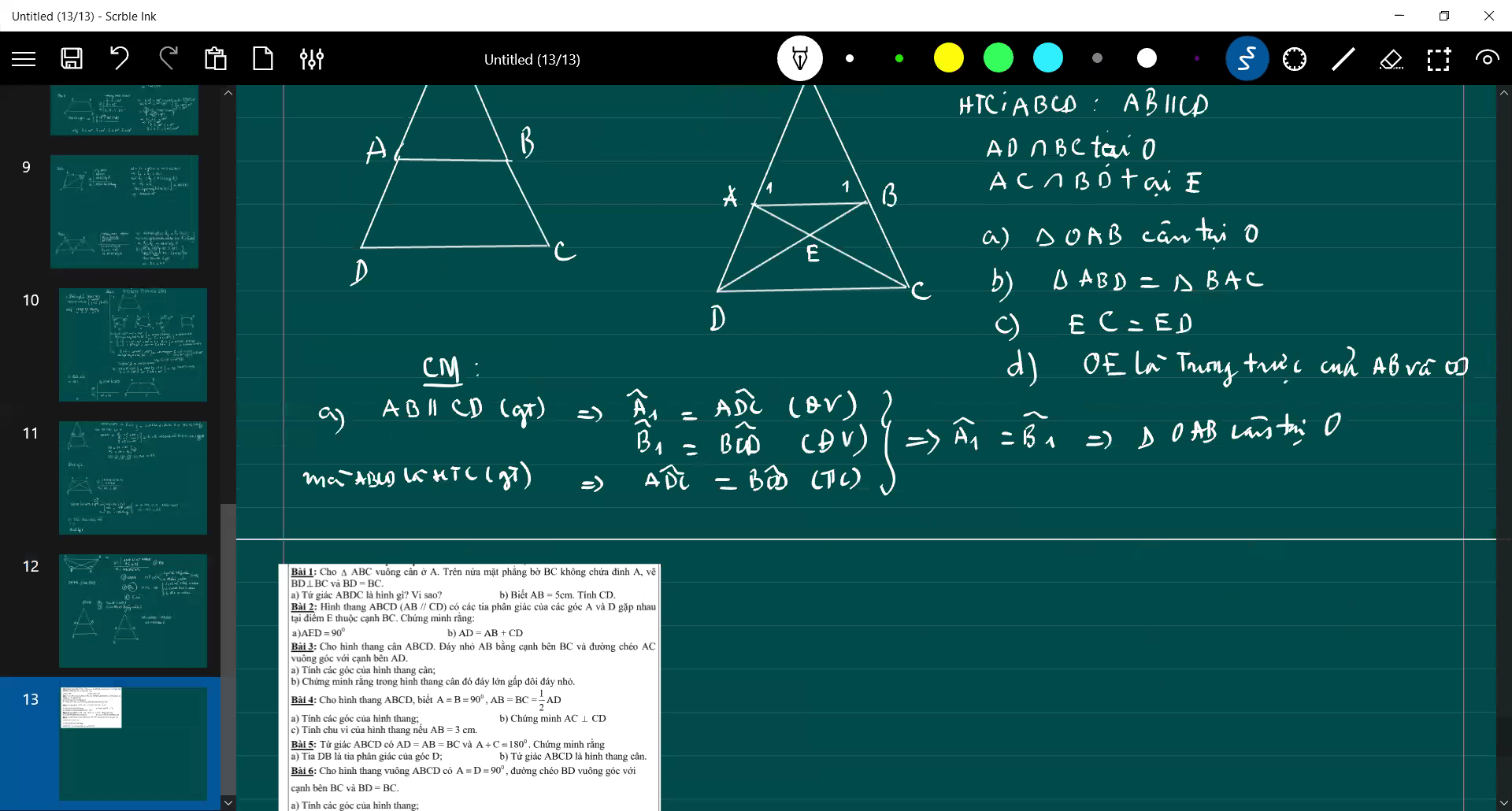
xin lỗi vì đã lm phiền mn ạ, giải hộ em với, em lm hết a với b rồi nên a chị nào giúp em câu c và d với ạ, đc sử dụng dữ kiện của câu trên nhé. GT ( đề bài ) ở bên phải hình vẽ ạ. HTC là hình thag cân ạ, còn cái (n) trong GT là cắt >< Mong mn giúp e ạ
cho hình thang cân MNPQ (Mn// PQ) có MN<PQ gọi E và D lần lượt là hình chiếu của M,N trên đường thẳng t kèm cả hình vẽ nữa ạ (mong có câu trả lời sớm cảm mn đã giúp)
Bài 22: a) Biết ít nhất mấy góc của hình thang cân thì tính được các góc cònlại b) Một hình thang cân có một góc bằng 70°. Đó là góc ở đáy lớn hay đáy nhỏ ? Tính các góc còn lại.(giải chi tiết hộ mình nha thank)
Bài 1: Cho hình thang cân ABCD ( AB // CD) Gọi E là giao điểm của AC và BD. Chứng minh EA = EB.
Bài 2: Cho hình thang cân ABCD (AB//CD) có AB=3,BC=CD=13(cm). Kẻ các đường cao AK và BH.
a) Chứng minh rằng CH=DK.
b) Tính độ dài BH.
Bài 3: Hình thang cân ABCD (AB//CD) có Cˆ=600, DB là tia phân giác của góc D, AB=4cm.
a) Chứng minh rằng BD vuông góc với BC.
b) Tính chu vi hình thang.
Bài 4 : Cho hình thang MNPQ (MN là đáy nhỏ) có 2 đường chéo MP và NQ cắt nhau tại O và NMPˆ=MNQˆA.
a) Chứng minh tam giác OMN và OPQ cân tại O.
b) Chứng minh tứ giác MNPQ là hình thang cân.
c) Qua O vẽ đường thẳng EF//QP (E∈MQ,F∈NP). Chứng minh MNFE, FEQP là những hình thang cân.
Bài 5: Cho hình thang cân ABCD (AB//CD, AB < CD). AD cắt BC tại O.
a) Chứng minh rằng ΔOAB cân.
b) Gọi I, J lần lượt là trung điểm của AB và CD. Chứng minh rằng ba điểm I, J, O thẳng hàng.
c) Qua điểm M thuộc cạnh AC, vẽ đường thẳng song song với CD, cắt BD tại N. Chứng minh rằng MNAB, MNDC là các hình thang cân.
1, Cho A= x-2.\(\sqrt{x-1}\)
Tính A khi x=\(\frac{53}{9-2\sqrt{7}}\)
2, Cho A=\(\frac{\sqrt{x}}{2\sqrt{x}-1}\)
Tính A khi x thỏa mãn x\(^2\) =\(\frac{1}{6}\)
3, Rút gọn:
A=\(\sqrt{1+\frac{1}{2}+\frac{1}{3^2}}+\sqrt{1+\frac{1}{3^2}+\frac{1}{4^2}}+...+\sqrt{1+\frac{1}{2005^2}+\frac{1}{2006^2}}\)
4, Cho A= \(\frac{\sqrt{x}}{\sqrt{x}-3}+\frac{\sqrt{x}+1}{\sqrt{x}+3}-\frac{2\sqrt{x}}{\sqrt{x}-1}\)
B= \(\frac{-x+14\sqrt{x}+3
}{x\sqrt{x}-4x+3\sqrt{x}}\)
a,Tìm đkxđ của A và B
b,Rút gọn M= A:B
Bạn nào làm được mong hãy bỏ ra một chút thời gian giải hộ mình dù chỉ 1 bài hay 1 ý thôi ạ
Mình xin cảm ơn mọi người!
2. Cho hình thang cân ABCD (AB // CD) có
A D = 3
. Tính các góc của hình thang cân.
3. Cho hình thang cân ABCD (AB // CD) có AH và BK là hai đường cao của hình thang.
a) Chứng minh DH = .
2
CD AB −
b) Biết AB = 6 cm, CD = 14 cm, AD = 5 cm, tính DH, AH và diện tích hình thang cân
ABCD.
4. Cho hình thang cân ABCD (AB//CD) có
0 A B = = 60
, AB = 4,5cm; AD = BC = 2 cm. Tính
độ dài đáy CD và diện tích hình thang cân ABCD.
5. Cho tam giác ABC cân tại A có BD và CE là hai đường trung tuyến của tam giác.
Chứng minh BCDE là hình thang cân.
6. Cho tam giác ABC cân tại A có BH và CK là hai đường cao của tam giác. Chứng minh
BCHK là hình thang cân.
7. Cho tam giác ABC cân tại A, có M là trung điểm của BC. Kẻ tií Mx song song với AC cắt AB
tại E và tia My song song với AB cắt AC tại F. Chứng minh:
a) EF là đường trung bình của tam giác ABC;
b) AM là đường trung trực của EF.
8. Cho tam giác ABC, có AM là trung tuyến ứng với BC. Trên cạnh AB lấy điểm D và E sao cho
AD = DE = EB. Đoạn CD cắt AM tại I. Chứng minh:
a) EM song song vói DC;
b) I là trung điểm của AM;
Giúp em với ạ
trên đoạn thẳng AB lấy M( MA>MB ) trên cừng một nữa mặt phẳng bờ AB vẽ các tam giác đều AMC; BMD. gọi E,F,I,K theo thứ tự là trung điểm của CM,CB,DM,DA. Chứng minh : EFIK là hình thang cân và KF= 1/2 CD
