Đặt \(f\left(\left|x\right|\right)=t\Rightarrow t^2+\left(m-2\right)t+m-3=0\) (1)
Do \(a-b+c=0\Rightarrow\left(1\right)\) luôn có 2 nghiệm \(\left[{}\begin{matrix}t=-1\\t=3-m\end{matrix}\right.\)
Đây là đồ thị hàm \(y=f\left(\left|x\right|\right)\)
Nhìn vào đồ thị, ta thấy \(t=1\) cho đúng 2 nghiệm
Do đó, để pt đã cho có 6 nghiệm pb thì \(t=3-m\) phải cho 4 nghiệm pb
\(\Rightarrow-1< 3-m< 3\Rightarrow0< m< 4\)
Có 3 giá trị nguyên của m thỏa mãn
https://i.imgur.com/d2B7XuA.png
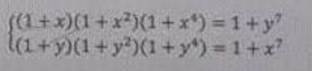mọi người giúp em giải hệ này với
giúp em với ạ