Xét hàm \(f\left(x\right)=\dfrac{1}{9^x-3}+\dfrac{1}{3^x-9}\) có \(f'\left(x\right)=-\dfrac{9^x.ln9}{\left(9^x-3\right)^2}-\dfrac{3^x.ln3}{\left(3^x-9\right)^2}< 0\)
\(\Rightarrow\) Hàm luôn nghịch biến trên miền xác định
\(\lim\limits_{x\rightarrow-\infty}f\left(x\right)=-\dfrac{1}{3}-\dfrac{1}{9}=-\dfrac{4}{9}\) ; \(\lim\limits_{x\rightarrow+\infty}f\left(x\right)=0\) ; \(f\left(4\right)>0\)
\(\lim\limits_{x\rightarrow0,5^+}f\left(x\right)=+\infty;\lim\limits_{x\rightarrow0,5^-}f\left(x\right)=-\infty;\lim\limits_{x\rightarrow2^-}f\left(x\right)=-\infty;\lim\limits_{x\rightarrow2^+}f\left(x\right)=+\infty\)
BBT:
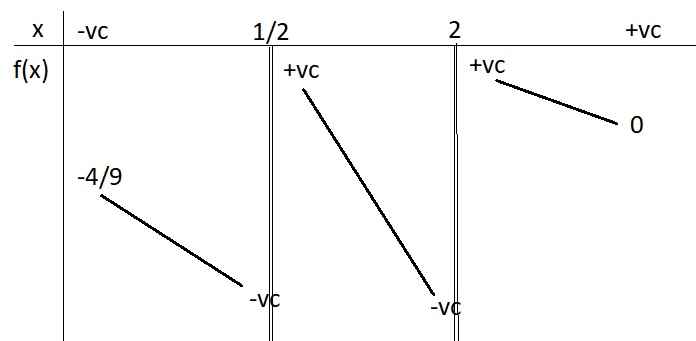
Xét hàm \(g\left(x\right)=x+\left|x-4\right|+a=\left\{{}\begin{matrix}a+4\text{ nếu }x\le4\\2x+a-4\text{ nếu }x\ge4\end{matrix}\right.\)
Từ BBT ta thấy:
- Nếu \(a\ge-3\Rightarrow g\left(x\right)\) cắt f(x) tại 2 điểm phân biệt thỏa mãn \(x< 4\)
- Nếu \(a=-4\Rightarrow g\left(x\right)\) cắt f(x) tại 2 điểm pb thỏa mãn \(x_1< 4< x_2\)
- Nếu \(a\le-5\) \(\Rightarrow g\left(x\right)\) cắt f(x) tại 3 điểm pb thỏa mãn \(x_1< x_2< 4< x_3\) (loại)
Vậy \(a=\left\{-1;-2;-3;-4\right\}\)









