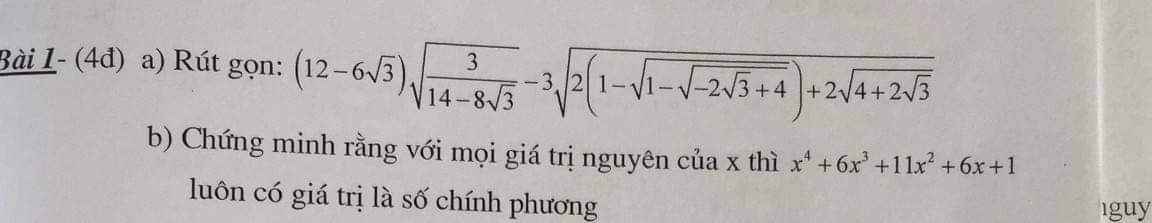a: Ta có: \(\left(12-6\sqrt{3}\right)\cdot\sqrt{\dfrac{3}{14-8\sqrt{3}}}-3\cdot\sqrt{2\left(1-\sqrt{1-\sqrt{4-2\sqrt{3}}}\right)+2\sqrt{4+2\sqrt{3}}}\)
\(=\left(3-\sqrt{3}\right)\cdot\dfrac{\sqrt{3}}{2\sqrt{2}-\sqrt{6}}-3\cdot\sqrt{2\cdot\left(1-\sqrt{1-\sqrt{3}+1}\right)+2\cdot\left(\sqrt{3}+1\right)}\)
\(=\left(3-\sqrt{3}\right)\cdot\dfrac{\sqrt{6}\left(2+\sqrt{3}\right)}{2}-3\cdot\sqrt{\left(2-\sqrt{2}\cdot\sqrt{4-2\sqrt{3}}\right)+2\sqrt{3}+2}\)
\(=\dfrac{\left(3\sqrt{6}-3\sqrt{2}\right)\left(2+\sqrt{3}\right)}{2}-3\cdot\sqrt{2-\sqrt{2}\left(\sqrt{3}+1\right)+2\sqrt{3}+2}\)
\(=\dfrac{3\sqrt{6}+3\sqrt{2}}{2}-3\cdot\sqrt{2-\sqrt{6}-\sqrt{2}+2\sqrt{3}+2}\)
Đến đây thì xin lỗi bạn, mình thua
b: Ta có: \(x^4+6x^3+11x^2+6x+1\)
\(=x^4+3x^3+x^2+3x^3+9x^2+3x+x^2+3x+1\)
\(=\left(x^2+3x+1\right)^2\) là số chính phương(đpcm)