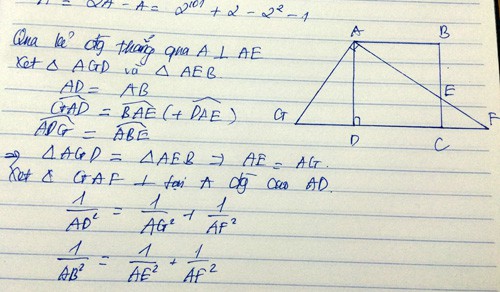Bài 1: Một số hệ thức về cạnh và đường cao trong tam giác vuông
Các câu hỏi tương tự
Qua đỉnh A của hình vuông ABCD cạnh bằng a, vẽ đường thẳng cắt BC ở E và cắt đường thẳng DC ở F. Chứng minh: \(\dfrac{1}{AE^{2^{ }}}+\dfrac{1}{ÀF^2}=\dfrac{1}{a^2}\)
help me
Cho hình bình hành ABCD. Hai đường thẳng đi qua tâm của hình bình hành chia nó thành bốn tứ giác có diện tích bằng nhau. Đường thẳng thứ nhất cắt BC tại E, đường thẳng thứ 2 cắt CD tại F. Chứng minh E chia cạnh BC và F chia cạnh CD theo cùng một tỉ số.
cho hcn abcd (ab<ad). Qua a vẽ đường thẳng vuông góc với bd, đường thẳng này cắt bd,cd,bc lần lượt tại h,e,f
1/cm tg fhb đồng dạng tg dhe
2/ cm hd.hb=he.hf
Cho tam giác ABC vuông tại A có AB=9cm,AC=12cm,đường cao AH.Tính BC,AH,BH,CH.
Cho tam giác ABC vuông tại A,đường cao AH chia cạnh huyền BC thành hai đoạn BH,CH có độ dài lần lượt là 4 cm,9cm.Gọi D,E là hình chiếu của H trên AB,AC
a) Tính độ dài AB,AC
b)Tứ giác ADHE là hình gì
c)Tính độ dài DE,số đo góc B, góc C
Mọi người ơiii giúp mình vớii!!!
Cho hình thang vuông ABCD. Góc A=góc D (=90 độ). Biết AB=9cm; CD=16cm; BC=25cm. Trên BC lấy E sao cho BE=BA. Tính:
a) Góc AED
b) Diện tích ABCD; diện tích tam giác AED
Cho hình vuông ABCD lấy điểm M ∈ BC vẽ AN ⊥ AM; N ∈ CD; tia AM cắt đường thẳng CD tại E.a) ΔANM là tam giác gì?b) Cmr: khi điểm M di động trên cạnh BC thì dfrac{1}{AM^2}+dfrac{1}{AE^2}không đổi A B C D N M
Đọc tiếp
Cho hình vuông ABCD lấy điểm M ∈ BC vẽ AN ⊥ AM; N ∈ CD; tia AM cắt đường thẳng CD tại E.
a) ΔANM là tam giác gì?
b) Cmr: khi điểm M di động trên cạnh BC thì \(\dfrac{1}{AM^2}+\dfrac{1}{AE^2}\)không đổi
Cho tam giác ABC vuông tại A, đường cao AH. E, F lần lượt là hình chiếu của H trên AB, AC. Gọi M là trung điểm BC. Chứng minh \(S_{AEMF}=\dfrac{1}{2}S_{ABC}\)
Cho hình vuông ABCD trên CD lấy điểm I, AI cắt BC tại N
Cmr: \(\dfrac{1}{AB^2}\) = \(\dfrac{1}{AI^2}\) +\(\dfrac{1}{AN^2}\)
AB2 = BN . DI
Giúp mình với ạ mình đang cần gấp !!!!!