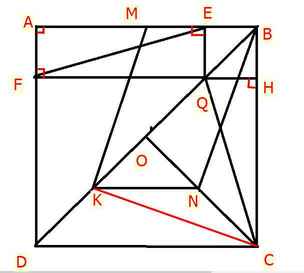
a) Ta có : \(\widehat{AEQ}=\widehat{EAF}=\widehat{AFQ}=90\)
➜ AEQF là hình chữ nhật ( DHNB hình chữ nhật )
b) Vì ABCD là hình vuông ➝ \(\widehat{ABD}=45\) ↔ \(\widehat{EBQ}=45\)
Mà ΔEBQ vuông tại E
➜ ΔEBQ vuông cân tại E
➝ EB = EQ
Mà \(\left\{{}\begin{matrix}FQ=AE\\AE+EB=AB\end{matrix}\right.\)
➞ QE + QF = AB
d) Ta có : AB = DC ( ABCD là hình vuông )
⇔ \(\dfrac{1}{2}DC=\dfrac{1}{2}AB=BM\)
Xét tam giác DOC có : K, N là trung điểm OD , OC
=> KN = \(\dfrac{1}{2}DC\) , KN // DC
Mà \(\dfrac{1}{2}DC=\dfrac{1}{2}AB=BM\) , DC // BM
=> KN = BM , KN // BM
=> KNBM là hình bình hành ( BDNB hình bình hành )
e) Ta có : KN ⊥ BC ( KN // AB // FH , FH ⊥ BC )
Lại có : AC ⊥ BD ( ABCD là hình vuông )
↔ CN ⊥ BD
Xét tam giác BCK có : CN ⊥ BD ; KN ⊥ BC
→ N là trực tâm Δ BCK
→ BN ⊥ KC
Mà BN // MK ( MBNK là hình bình hành )
→ MK ⊥ KC
➢ ĐPCM

 help pls
help pls











