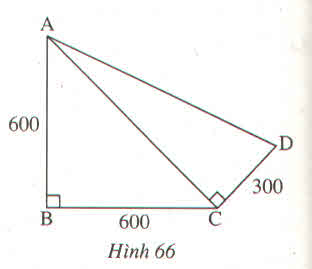
- Gọi quãng đường người thứ nhất đi là x ( km, x > 0 )
- Gọi quãng đường người thứ hai đi là y ( km, y > 0 )
Theo đề bài quãng đường người thứ hai đi gấp 2 lần quãng đường người thứ nhất đi \(y=2x\left(I\right)\)
- Áp dụng định lý pi - ta - go vào tam giác ABC vuông tại A ta được :
\(x^2+y^2=BC^2\)
=> \(x^2+y^2=15625\) ( II )
- Từ ( I ) và ( II ) ta có hệ phương trình : \(\left\{{}\begin{matrix}y=2x\\x^2+y^2=15625\end{matrix}\right.\)
=> \(\left\{{}\begin{matrix}y=2x\\x^2+4x^2=15625\end{matrix}\right.\)
=> \(\left\{{}\begin{matrix}y=2x\\x^2=3125\end{matrix}\right.\)
=> \(\left\{{}\begin{matrix}y=2.25\sqrt{5}=50\sqrt{5}\\x=25\sqrt{5}\end{matrix}\right.\) ( TM )
Vậy quãng đường người thứ hai đi là \(50\sqrt{5}\) km.