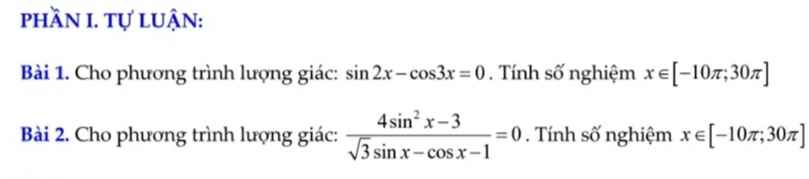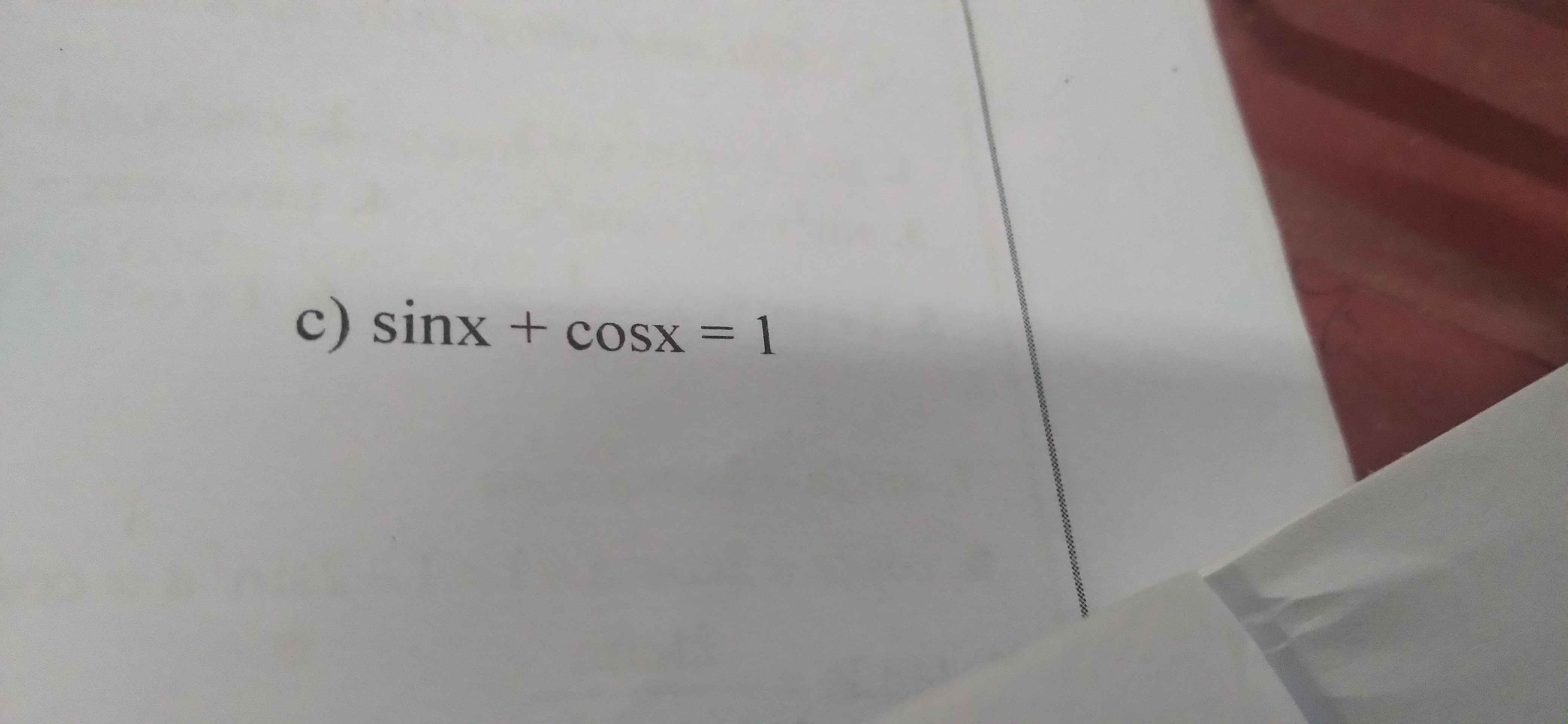1.
\(sin2x-cos3x=0\)
\(\Leftrightarrow cos3x=sin2x=cos\left(\dfrac{\pi}{2}-2x\right)\)
\(\Rightarrow\left[{}\begin{matrix}3x=\dfrac{\pi}{2}-2x+k2\pi\\3x=2x-\dfrac{\pi}{2}+n2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{10}+\dfrac{k2\pi}{5}\\x=-\dfrac{\pi}{2}+n2\pi\end{matrix}\right.\)
Do \(-10\pi\le x\le30\pi\)
\(\Rightarrow\left\{{}\begin{matrix}-10\pi\le\dfrac{\pi}{10}+\dfrac{k2\pi}{5}\le30\pi\\-10\pi\le-\dfrac{\pi}{2}+n2\pi\le30\pi\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}-\dfrac{101}{4}\le k\le\dfrac{299}{4}\\-\dfrac{19}{4}\le n\le\dfrac{61}{4}\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}k=\left\{-25;-24;...;74\right\}\\n=\left\{-4;-3;...;15\right\}\end{matrix}\right.\)
\(\Rightarrow\) Có \(74-\left(-25\right)+1+15-\left(-4\right)+1=120\) nghiệm trên đoạn đã cho
2.
ĐKXĐ: \(\sqrt{3}sinx-cosx\ne1\Leftrightarrow sin\left(x-\dfrac{\pi}{6}\right)\ne\dfrac{1}{2}\)
\(\Rightarrow\left\{{}\begin{matrix}x\ne\dfrac{\pi}{3}+k2\pi\\x\ne\pi+k2\pi\end{matrix}\right.\)
Phương trình trở thành:
\(4sin^2x-3=0\)
\(\Leftrightarrow2-2cos2x-3=0\)
\(\Leftrightarrow cos2x=-\dfrac{1}{2}\Rightarrow\left[{}\begin{matrix}2x=\dfrac{2\pi}{3}+k2\pi\\2x=-\dfrac{2\pi}{3}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{3}+k\pi\\x=-\dfrac{\pi}{3}+k\pi\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{3}+n2\pi\\x=\dfrac{4\pi}{3}+l2\pi\\x=-\dfrac{\pi}{3}+k\pi\end{matrix}\right.\)
Kết hợp ĐKXĐ \(\Rightarrow\left[{}\begin{matrix}x=\dfrac{4\pi}{3}+l2\pi\\x=-\dfrac{\pi}{3}+k\pi\end{matrix}\right.\)
\(-10\pi\le x\le30\pi\Rightarrow\left\{{}\begin{matrix}-10\pi\le\dfrac{4\pi}{3}+l2\pi\le30\pi\\-10\pi\le-\dfrac{\pi}{3}+k\pi\le30\pi\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}l=\left\{-5;-4;...;14\right\}\\k=\left\{-9;-8;...;30\right\}\end{matrix}\right.\) có 60 nghiệm