
a, vì M là trung điểm của AC nên AM = CM
xét \(\Delta ADM\) và \(\Delta BCM\)
có \(\left\{{}\begin{matrix}BM=DM\left(gt\right)\\\widehat{BMC}=\widehat{AMD}\\AM=CM\left(cmt\right)\end{matrix}\right.\) ( 2 góc đối đỉnh )
=> \(\Delta ADM=\Delta BCM\left(c.g.c\right)\) (đpcm)
=>\(\widehat{DAM}=\widehat{BCM}\) ( 2 góc tương ứng )
mà hai góc trên nằm ở vị trí so le trong của hai đường thẳng AD và BC
=> AD // CB ( đpcm )
b, từ a có
\(\Delta ADM=\Delta BCM\left(c.g.c\right)\)
=> \(\widehat{ADM}=\widehat{CBM}\) ( 2 góc tương ứng ) (1)
xét \(\Delta ABM\) và \(\Delta DMC\)
có \(\left\{{}\begin{matrix}AM=CM\left(cmt\right)\\\widehat{AMB}=\widehat{DMC}\\BM=DM\left(gt\right)\end{matrix}\right.\) ( 2 góc đối đỉnh )
=> \(\Delta ABM=\Delta DMC\) (c.g.c)
=> \(\widehat{ABM}=\widehat{CDM}\) ( 2 góc tương ứng ) (2)
xét \(\Delta ABD\) và \(\Delta BCD\)
có \(\left\{{}\begin{matrix}\widehat{CBM}=\widehat{ADM}\left(1\right)\\BD\\\widehat{ABM}=\widehat{CDM}\left(2\right)\end{matrix}\right.\) là cạnh chung
=> \(\Delta ABD=\Delta BCD\left(g.c.g\right)\)
=> DA = DC ( 2 cạnh tương ứng )
=> tam giác ADC là tam giác cân tại D (đpcm)









 giúp em vs ạ
giúp em vs ạ


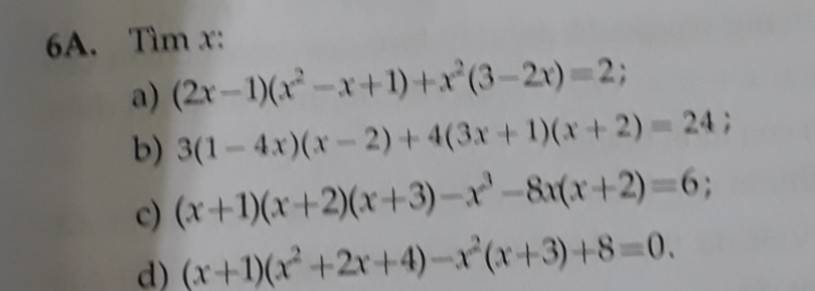 giúp em làm vs ạ
giúp em làm vs ạ





 mấy bạn xem giúp mk vs
mấy bạn xem giúp mk vs