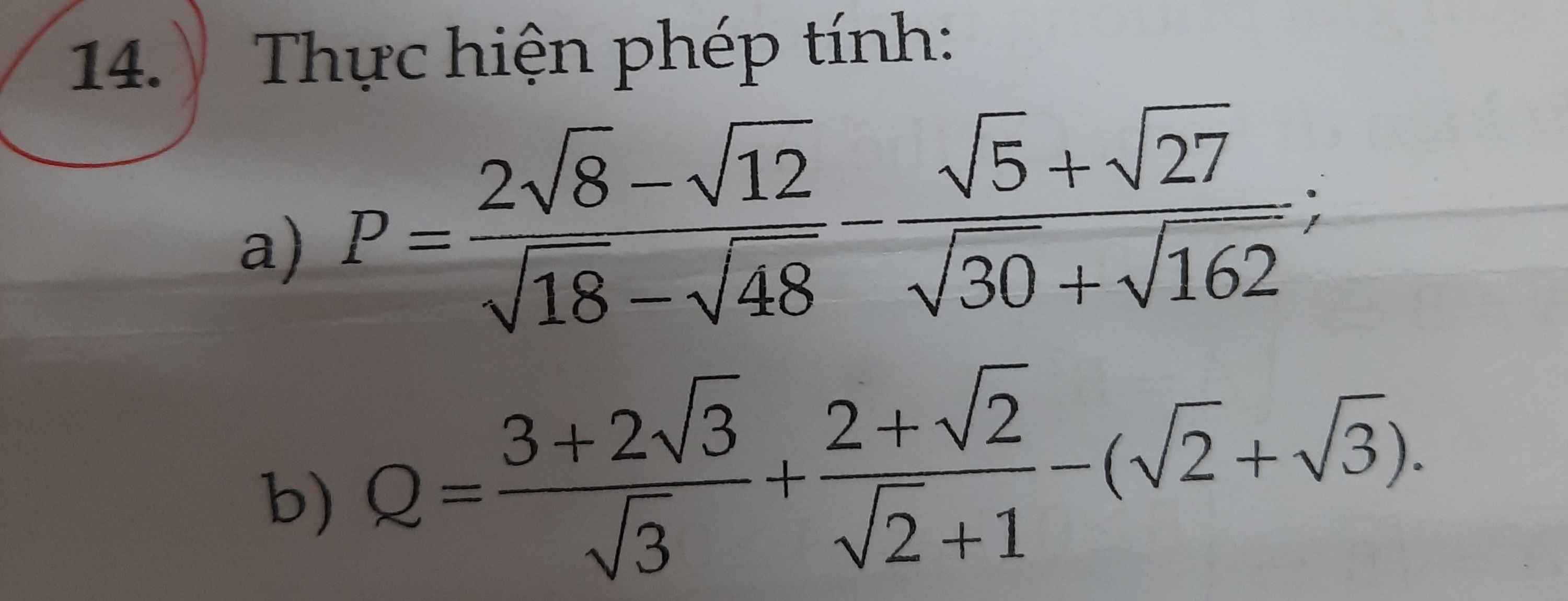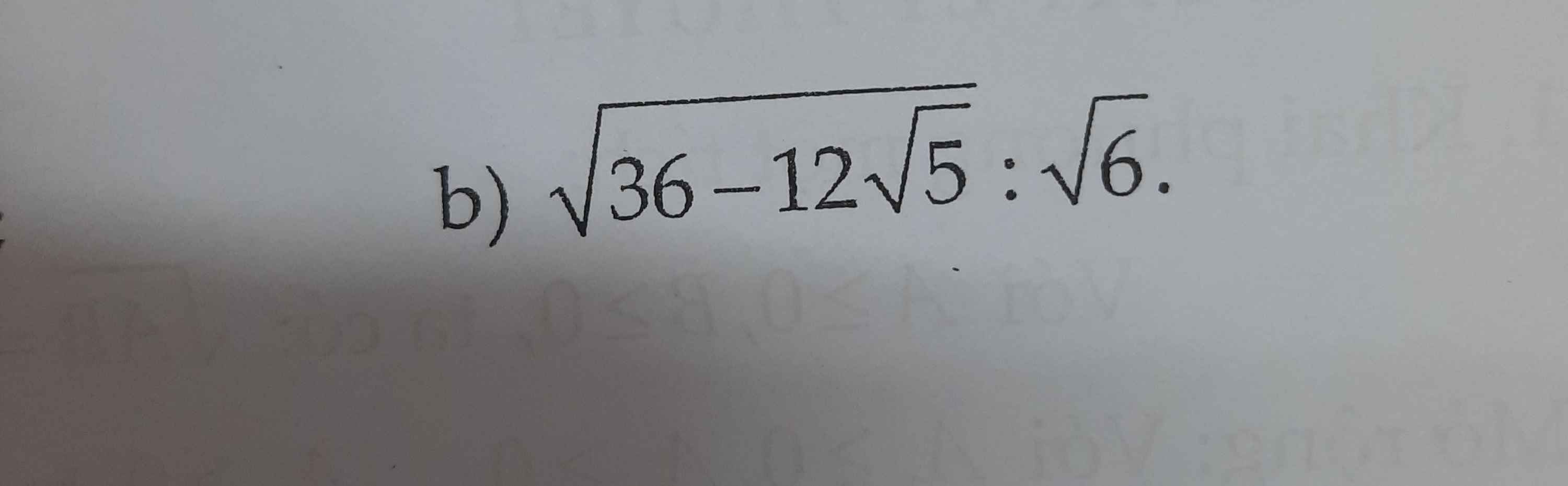Mình chỉ làm phần a, còn phần b có bạn phía dưới làm rồi.
a.
\(P=\frac{4\sqrt{2}-2\sqrt{3}}{3\sqrt{2}-4\sqrt{3}}-\frac{\sqrt{5}+\sqrt{27}}{\sqrt{30}+9\sqrt{2}}\)
\(=\frac{(4\sqrt{2}-2\sqrt{3})(3\sqrt{2}+4\sqrt{3})}{-30}-\frac{\sqrt{5}+\sqrt{27}}{\sqrt{6}(\sqrt{5}+\sqrt{27})}\)
\(=\frac{10\sqrt{6}}{-30}-\frac{1}{\sqrt{6}}=\frac{-\sqrt{6}}{3}-\frac{1}{\sqrt{6}}=\frac{-\sqrt{6}}{2}\)
a) Ta có: \(P=\dfrac{2\sqrt{8}-\sqrt{12}}{\sqrt{18}-\sqrt{48}}-\dfrac{\sqrt{5}+\sqrt{27}}{\sqrt{30}+\sqrt{162}}\)
\(=\dfrac{\sqrt{4}\left(2\sqrt{2}-\sqrt{3}\right)}{-\sqrt{6}\left(-\sqrt{3}+2\sqrt{2}\right)}-\dfrac{\sqrt{5}+\sqrt{27}}{\sqrt{6}\left(\sqrt{5}+\sqrt{27}\right)}\)
\(=\dfrac{-2-\sqrt{5}}{\sqrt{6}}\)
\(=\dfrac{-2\sqrt{6}-\sqrt{30}}{6}\)
b) Ta có: \(Q=\dfrac{3+2\sqrt{3}}{\sqrt{3}}+\dfrac{2+\sqrt{2}}{\sqrt{2}+1}-\left(\sqrt{2}+\sqrt{3}\right)\)
\(=\sqrt{3}+2+\sqrt{2}-\sqrt{2}-\sqrt{3}\)
=2