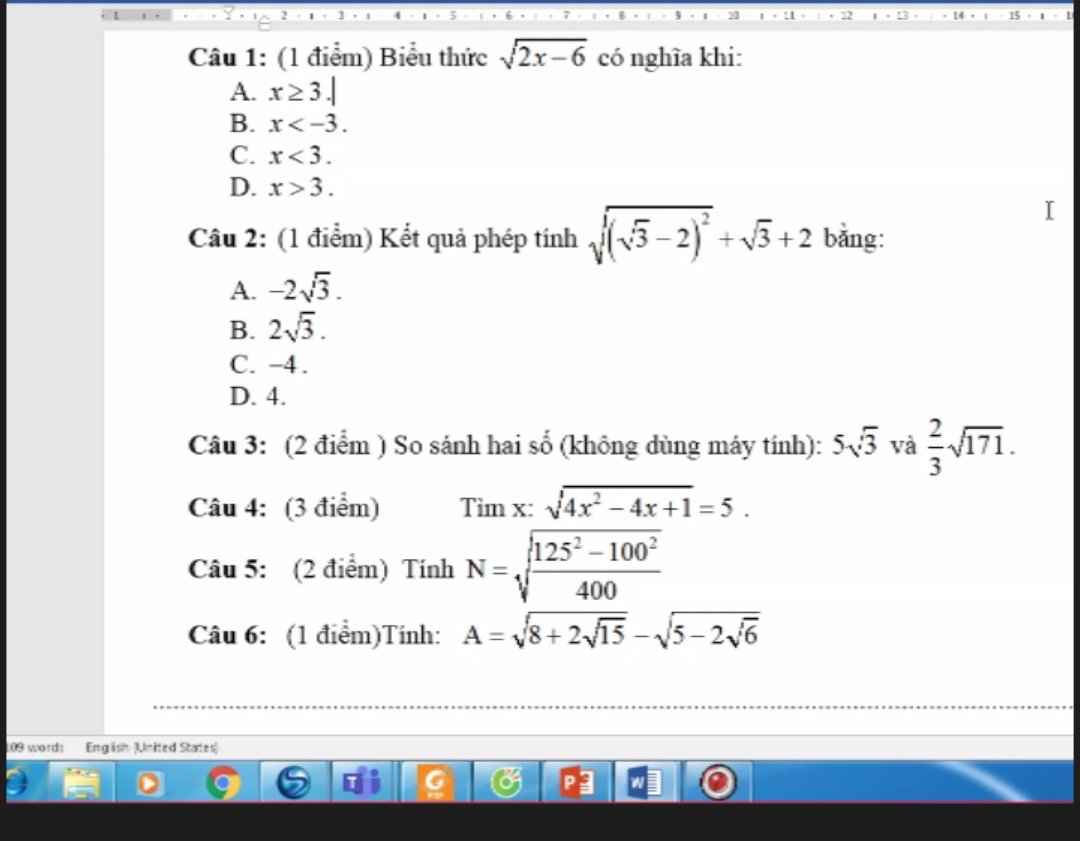
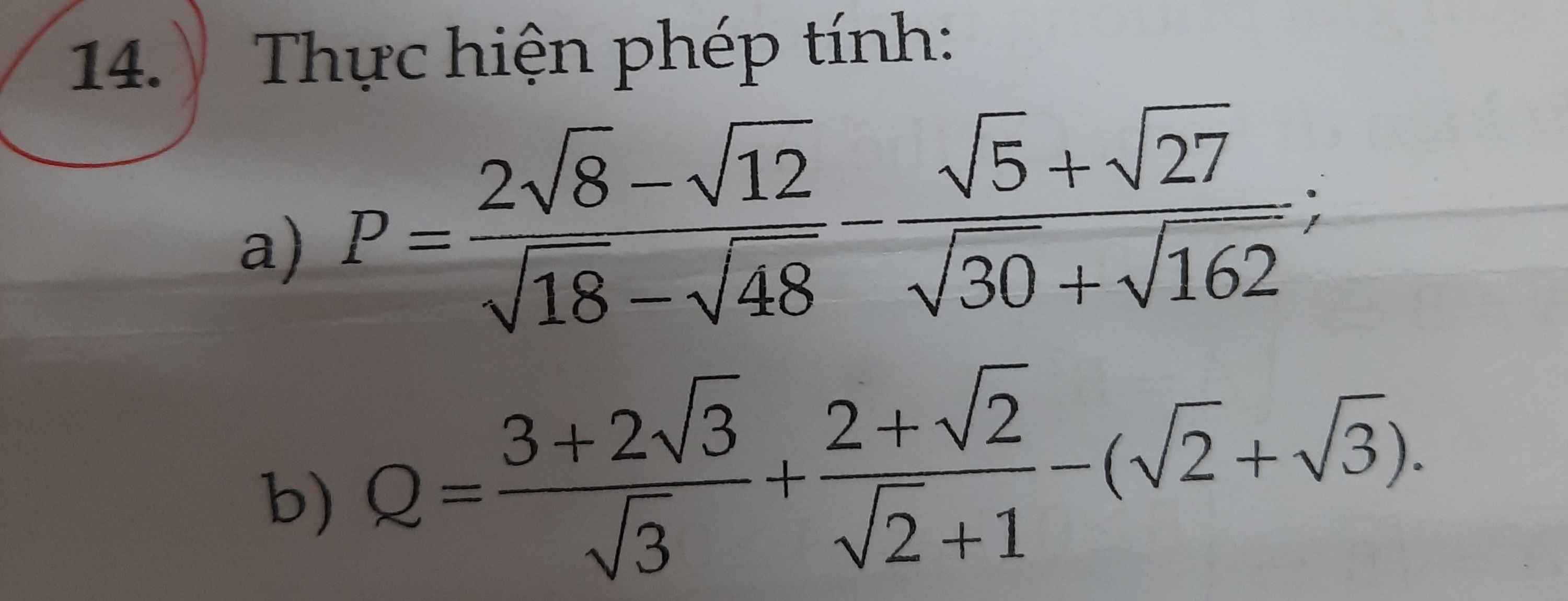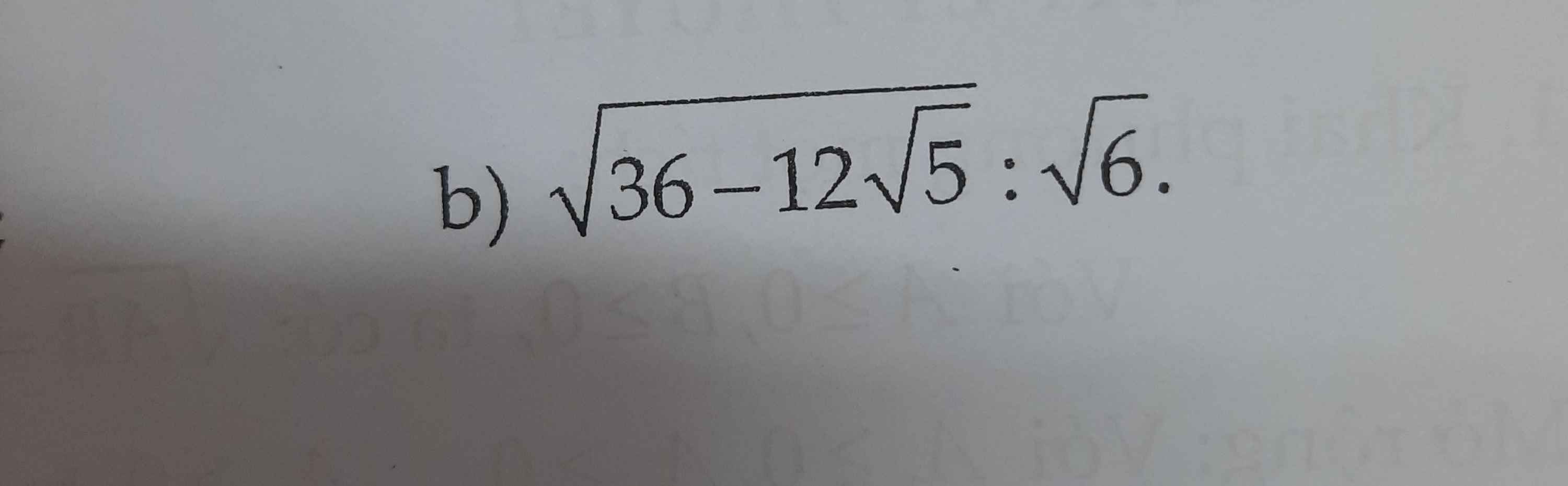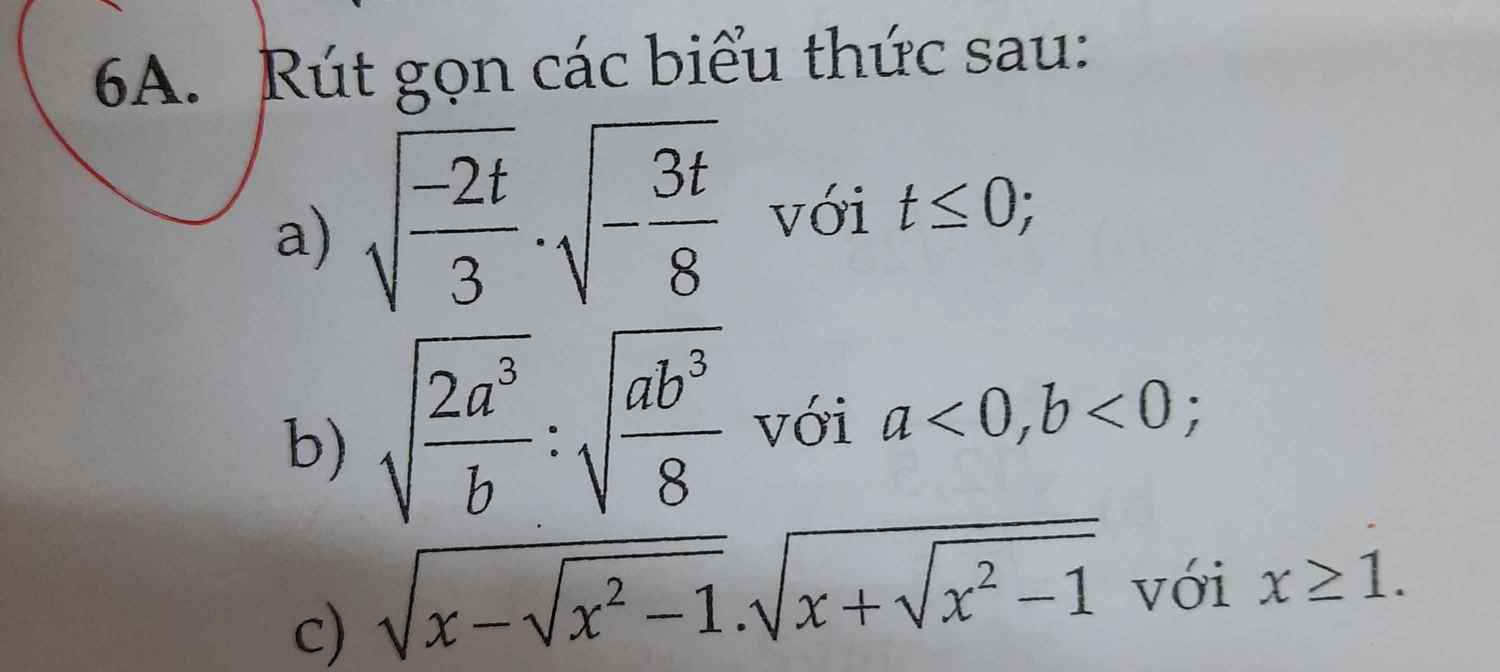\(1,A\\ 2,D\\ 3,\\ \left(5\sqrt{3}\right)^2=75< 76=\left(2\sqrt{19}\right)^2=\dfrac{2}{3}\sqrt{19\cdot9}=\dfrac{2}{3}\sqrt{171}\\ 4,\\ ĐK:x\in R\\ PT\Leftrightarrow\left|2x-1\right|=5\Leftrightarrow\left[{}\begin{matrix}2x-1=5\left(x\ge\dfrac{1}{2}\right)\\1-2x=5\left(x< \dfrac{1}{2}\right)\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=3\left(tm\right)\\x=-2\left(tm\right)\end{matrix}\right.\\ 5,N=\sqrt{\dfrac{\left(125-100\right)\left(125+100\right)}{400}}=\dfrac{\sqrt{25\cdot225}}{20}\\ N=\dfrac{\sqrt{25}\cdot\sqrt{225}}{20}=\dfrac{5\cdot15}{20}=\dfrac{15}{4}\)
\(6,\\ A=\sqrt{\left(\sqrt{3}+\sqrt{5}\right)^2}-\sqrt{\left(\sqrt{3}-\sqrt{2}\right)^2}\\ A=\sqrt{3}+\sqrt{5}-\sqrt{3}+\sqrt{2}=\sqrt{5}+\sqrt{2}\)