câu 1:
\(x=\dfrac{b^2+c^2-a^2}{2bc}=\dfrac{\left(b+c\right)^2-2bc-a^2}{2bc}\\ =\dfrac{\left(b+c\right)^2-a^2}{2bc}-1\)
\(xy=\left(\dfrac{\left(b+c\right)^2-a^2}{2bc}-1\right).\left(\dfrac{a^2-\left(b-c\right)^2}{\left(b+c\right)^2-a^2}\right)\\ =\dfrac{\left(\left(b+c\right)^2-a^2\right)\left(a^2-\left(b-c\right)^2\right)}{2bc\left(\left(b+c\right)^2-a^2\right)}-\dfrac{a^2-\left(b-c\right)^2}{\left(b+c\right)^2-a^2}\\ =\dfrac{a^2-\left(b-c\right)^2}{2bc}-\dfrac{a^2-\left(b-c\right)^2}{\left(b+c\right)^2-a^2}\)
\(x+y+xy=\dfrac{\left(b+c\right)^2-a^2}{2bc}-1+\dfrac{a^2-\left(b-c\right)^2}{\left(b+c\right)^2-a^2}+\dfrac{a^2-\left(b-c\right)^2}{2bc}-\dfrac{a^2-\left(b-c\right)^2}{\left(b+c\right)^2-a^2}\)
\(=\dfrac{\left(b+c\right)^2-a^2}{2bc}-1+\dfrac{a^2-\left(b-c\right)^2}{2bc}=\dfrac{a^2-\left(b-c\right)^2}{2bc}-\dfrac{a^2-\left(b-c\right)^2}{2bc}-1=-1\)
câu 3
\(\dfrac{\left(3x+1\right)}{\left(x+1\right)^3}=\dfrac{a}{\left(x+1\right)^3}+\dfrac{b}{\left(x+1\right)^2}\)
quy đồng và khử mẫu phương trình trên, ta được:
\(3x+1=a+b\left(x+1\right)\\ \Leftrightarrow3x+1=bx+a+b\)
\(\Rightarrow\left\{{}\begin{matrix}3x=bx\\1=a+b\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}3=b\\-2=a\end{matrix}\right.\)
vậy a=-2 và b=3
sách NÂNG CAO VÀ PHÁT TRIỂN TOÁN 8 có
tất cả các bài trên






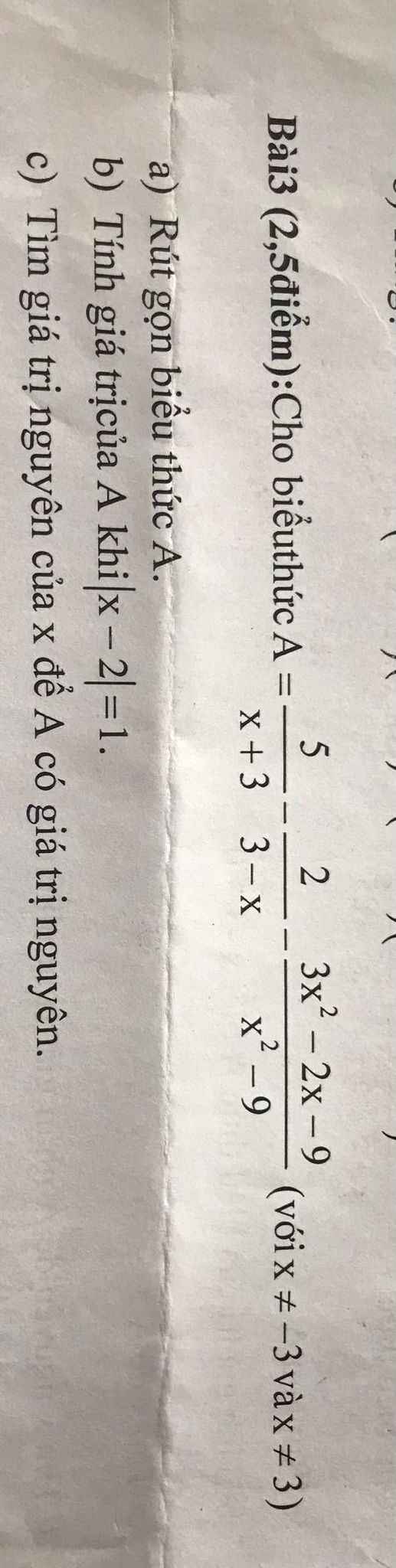






 Các bạn giải giúp mình với ạ, phần a ghi chi tiết bước giải hộ mình nhé. Mình cám ơn ạ! (Mai mình nộp rồi nên nhanh giúp mình ạ T.T)
Các bạn giải giúp mình với ạ, phần a ghi chi tiết bước giải hộ mình nhé. Mình cám ơn ạ! (Mai mình nộp rồi nên nhanh giúp mình ạ T.T)



