b) Ta có: \(2x-\left|3-x\right|=3\)
\(\Leftrightarrow\left|3-x\right|=2x-3\)
\(\Leftrightarrow\left[{}\begin{matrix}3-x=3-2x\left(x>3\right)\\3-x=2x-3\left(x\le3\right)\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}3-x-3+2x=0\\3-x-2x+3=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\left(loại\right)\\-3x=-6\end{matrix}\right.\Leftrightarrow x=2\left(nhận\right)\)
Vậy: S={2}
b) PT \(\Leftrightarrow\left|3-x\right|=2x-3\) \(\left(x\ge\dfrac{3}{2}\right)\)
\(\Rightarrow\left[{}\begin{matrix}3-x=2x-3\\3-x=3-2x\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-6\left(loại\right)\end{matrix}\right.\)
Vậy \(x=2\)









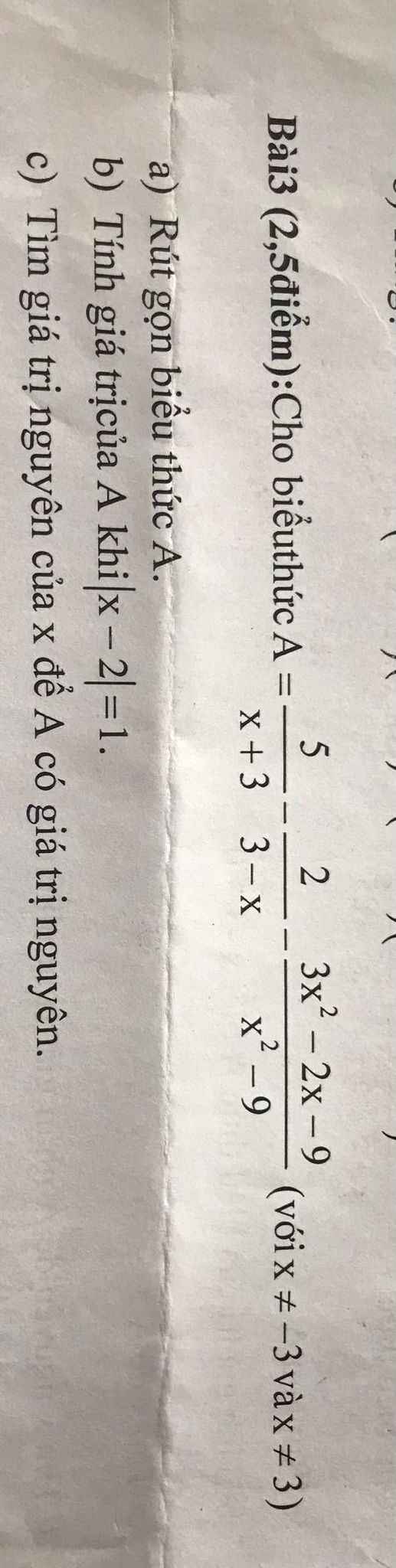



 Các bạn giải giúp mình với ạ, phần a ghi chi tiết bước giải hộ mình nhé. Mình cám ơn ạ! (Mai mình nộp rồi nên nhanh giúp mình ạ T.T)
Các bạn giải giúp mình với ạ, phần a ghi chi tiết bước giải hộ mình nhé. Mình cám ơn ạ! (Mai mình nộp rồi nên nhanh giúp mình ạ T.T)









