Bài 1:
a: A(-1;2); B(2;-2); C(-1;-3)
\(\overrightarrow{AB}=\left(3;-4\right)\)
=>VTPT là (4;3)
Phương trình đường thẳng AB là:
4(x+1)+3(y-2)=0
=>4x+4+3y-6=0
=>4x+3y-2=0
\(\overrightarrow{AC}=\left(0;-5\right)\)
=>VTPT là (5;0)
Phương trình AC là:
5(x+1)+0(y-2)=0
=>x+1=0
=>x=-1
\(\overrightarrow{BC}=\left(-3;-1\right)\)
=>VTPT là (1;-3)
Phương trình BC là:
1(x-2)+(-3)(y+2)=0
=>x-2-3y-6=0
=>x-3y-8=0
b: \(\overrightarrow{BC}=\left(-3;-1\right)\)
mà AH\(\perp\)BC
nên AH nhận \(\overrightarrow{BC}=\left(-3;-1\right)=\left(3;1\right)\) làm vecto pháp tuyến
Phương trình đường cao AH là:
3(x+1)+1(y-2)=0
=>3x+3+y-2=0
=>3x+y+1=0
\(\overrightarrow{AC}=\left(0;-5\right)\)
mà BK\(\perp\)AC
nên BK nhận \(\overrightarrow{AC}=\left(0;-5\right)\) làm vecto pháp tuyến
Phương trình đường cao BK là:
0(x-2)+(-5)(y+2)=0
=>-5(y+2)=0
=>y=-2
Tọa độ trọng tâm của ΔABC là:
\(\left\{{}\begin{matrix}x=\dfrac{-1+2+\left(-1\right)}{3}=0\\y=\dfrac{2+\left(-2\right)+\left(-3\right)}{3}=-1\end{matrix}\right.\)
c: Tọa độ M là:
\(\left\{{}\begin{matrix}x=\dfrac{2+\left(-1\right)}{2}=\dfrac{1}{2}\\y=\dfrac{-2+\left(-3\right)}{2}=-\dfrac{5}{2}\end{matrix}\right.\)
Vậy: A(-1;2); M(0,5;-2,5)
\(\overrightarrow{AM}=\left(1,5;-4,5\right)=\left(1;-3\right)\)
=>VTPT là (3;1)
Phương trình đường trung tuyến AM là:
3(x+1)+1(y-2)=0
=>3x+3+y-2=0
=>3x+y+1=0
Tọa độ trung điểm N của AB là:
\(\left\{{}\begin{matrix}x=\dfrac{-1+2}{2}=0,5\\y=\dfrac{2+\left(-2\right)}{2}=0\end{matrix}\right.\)
N(0,5;0); C(-1;-3)
\(\overrightarrow{CN}=\left(1,5;3\right)=\left(1;2\right)\)
=>VTPT là (-2;1)
Phương trình đường trung tuyến CN là:
-2(x+1)+1(y+3)=0
=>-2x-2+y+3=0
=>-2x+y+1=0
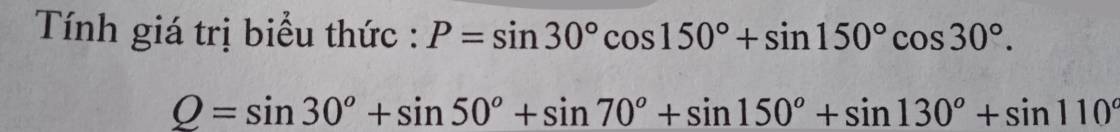
Giải giúp mình từ bài 3 đến bài 6 ạ 
