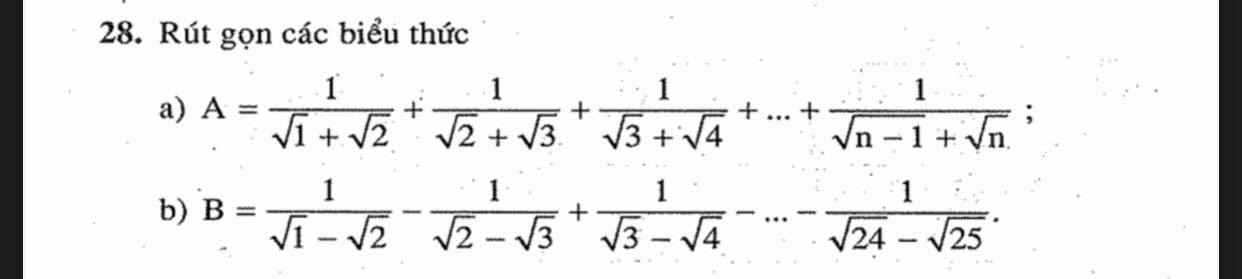\(a,\) Ta có \(\dfrac{1}{\sqrt{n-1}+\sqrt{n}}\)
\(=\dfrac{\sqrt{n-1}-\sqrt{n}}{\left(\sqrt{n-1}+\sqrt{n}\right)\left(\sqrt{n-1}-\sqrt{n}\right)}\\ =\dfrac{\sqrt{n-1}-\sqrt{n}}{n-1-n}=\sqrt{n}-\sqrt{n-1}\)
Thay vào A
\(A=\dfrac{1}{1+\sqrt{2}}+\dfrac{1}{\sqrt{2}+\sqrt{3}}+...+\dfrac{1}{\sqrt{n-1}+\sqrt{n}}\\ A=\sqrt{2}-1+\sqrt{3}-\sqrt{2}+...+\sqrt{n}-\sqrt{n-1}\\ A=\sqrt{n}-1\)
\(b,\) Ta có \(\dfrac{1}{\sqrt{n-1}-\sqrt{n}}=\dfrac{\sqrt{n-1}+\sqrt{n}}{\left(\sqrt{n-1}-\sqrt{n}\right)\left(\sqrt{n-1}+\sqrt{n}\right)}\)
\(=\dfrac{\sqrt{n-1}+\sqrt{n}}{n-1-n}=-\sqrt{n-1}-\sqrt{n}\)
Thay vào B
\(B=\dfrac{1}{\sqrt{1}-\sqrt{2}}-\dfrac{1}{\sqrt{2}-\sqrt{3}}-...-\dfrac{1}{\sqrt{24}-\sqrt{25}}\\ B=-1-\sqrt{2}-\left(-\sqrt{2}-\sqrt{3}\right)-...-\left(-\sqrt{24}-\sqrt{25}\right)\\ B=-1-\sqrt{2}+\sqrt{2}+\sqrt{3}-\sqrt{3}-\sqrt{4}+...+\sqrt{24}+\sqrt{25}\\ B=\sqrt{25}-1\)