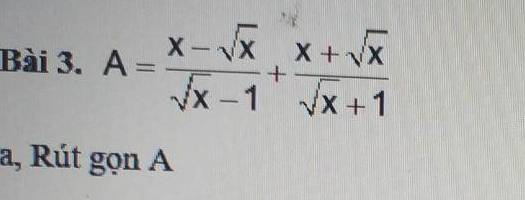Đặt\(\begin{cases} x+y=S \\ xy=P \end{cases}\)
Ta có:\(\begin{cases} S-2P=0 \\ S-P^2=\sqrt{(P-1)^2+1} \end{cases}\)
\(\Leftrightarrow\)\(\begin{cases} S=2P \\ 2P-P^2=\sqrt{(P-1)^2+1} \end{cases}\)
\(\Leftrightarrow\)\(\begin{cases} S=2P \\ (2P-P^2)^2=(P-1)^2+1 \end{cases}\)
\(\Leftrightarrow\)\(\begin{cases} S=2P \\ 4P^2-4P^3+P^4=P^2-2P+2 \end{cases}\)
\(\Leftrightarrow\)\(\begin{cases} S=2P \\ P^4-4P^3+3P^2+2P-2=0 \end{cases}\)
\(\Leftrightarrow\)\(\begin{cases} S =2+2\sqrt{3}\\ P=1+\sqrt{3} \end{cases}\)(1)hoặc\(\begin{cases} S=2 \\ P=1 \end{cases}\)(2)hoặc\(\begin{cases} S=2-2 \sqrt{3}\\ P=1-\sqrt{3} \end{cases}\)(3)
Còn lại là thay vào biểu thức x2-Sx+P=0 thôi













 Giúp mình giải 2 câu này với. Mình cảm ơn
Giúp mình giải 2 câu này với. Mình cảm ơn