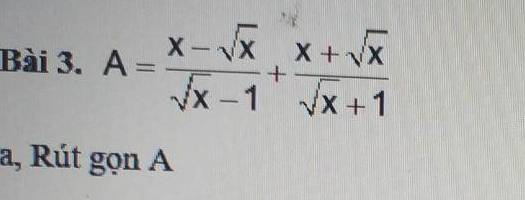\(P=\dfrac{x}{1-x^2}+\dfrac{y}{1-y^2}+\dfrac{z}{1-z^2}\)
Ta có: \(2x^2.\left(1-x^2\right)\left(1-x^2\right)\le\dfrac{1}{27}\left(2x^2+1-x^2+1-x^2\right)^3=\dfrac{8}{27}\)
\(\Rightarrow x^2\left(1-x^2\right)^2\le\dfrac{4}{27}\)
\(\Rightarrow x\left(1-x^2\right)\le\dfrac{2}{3\sqrt{3}}\)
\(\Rightarrow\dfrac{x}{1-x^2}\ge\dfrac{3\sqrt{3}}{2}x^2\)
Tương tự và cộng lại:
\(P\ge\dfrac{3\sqrt{3}}{2}\left(x^2+y^2+z^2\right)=...\)












 Giúp mình giải 2 câu này với. Mình cảm ơn
Giúp mình giải 2 câu này với. Mình cảm ơn

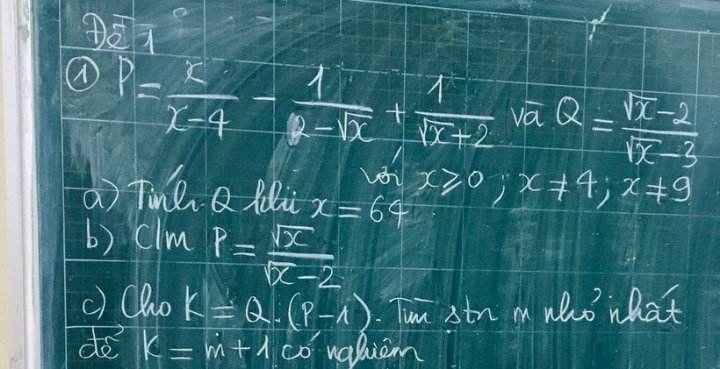 giúp mình câu c với ạ, mình cảm ơn nhiều
giúp mình câu c với ạ, mình cảm ơn nhiều