Chương 2: TÍCH VÔ HƯỚNG CỦA HAI VECTƠ VÀ ỨNG DỤNG
Các câu hỏi tương tự
cho tứ giác ABCD . Gọi M , N lần luợt là trung điểm của AC và BD . Chứng minh rằng : AB2 + BC2 + CD2 +DA2 = AC2 + BD2 + 4MN2
Cho hình bình hành ABCD. Gọi O là giao điểm của hai đường chéo AC và BD; N là trung điểm của cạnh CD; P là điểm thỏa mãn hệ thức (1.0 điểm). Chứng minh đẳng thức .
Đọc tiếp
Cho hình bình hành ABCD. Gọi O là giao điểm của hai đường chéo AC và BD; N là trung điểm của cạnh CD; P là điểm thỏa mãn hệ thức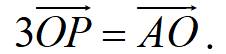
(1.0 điểm). Chứng minh đẳng thức .
cho hbh abcd gọi m n lần lượt là hai điểm nằm trên hai cạnh ab và cd sao cho ab =3AM CD=2CN Biểu diễn vectơ AN qua các vectơ AB và AC
Cho hình bình hành ABCD. Gọi N là trung điểm cạnh CD. Trên cạnh AC lấy điểm M sao cho AM = 2MC; Phân tích các vec tơ sau theo hai véc tơ ABvà AD
a. vecto ac
b) vecto AM
c) vecto an
Cho hình chữ nhật ABCD tâm O. Gọi M, N lần lượt là trung điểm của OA và CD. Biết
overrightarrow{MN} a.overrightarrow{AB}+b.overrightarrow{AD}. Tính a + b.
A. a + b 1 B. a + b dfrac{1}{2} C. a + b dfrac{3}{4} D. a + b dfrac{1}{4}
Đọc tiếp
Cho hình chữ nhật ABCD tâm O. Gọi M, N lần lượt là trung điểm của OA và CD. Biết
\(\overrightarrow{MN}\) = \(a.\overrightarrow{AB}+b.\overrightarrow{AD}\). Tính a + b.
A. a + b = 1 B. a + b = \(\dfrac{1}{2}\) C. a + b = \(\dfrac{3}{4}\) D. a + b = \(\dfrac{1}{4}\)
Cho tứ giác ABCD nội tiếp (O;R). AC vuông góc với BD và AC cắt BD tại I. Gọi trung điểm của AB là M. Chứng minh rằng MI vuông góc với DC
Cho hình thang vuông ABCD,đường cao AB2a,đáy lớn BC3a
a) tính overrightarrow{AB}.overrightarrow{CD}
overrightarrow{BD}.overrightarrow{BC}
overrightarrow{AC}.overrightarrow{BD}
b)gọi I là trung điểm của CD tính overrightarrow{AI.}overrightarrow{BD}và suy ra góc của 2 vecto AI và BD
Đọc tiếp
Cho hình thang vuông ABCD,đường cao AB=2a,đáy lớn BC=3a
a) tính \(\overrightarrow{AB}\).\(\overrightarrow{CD}\)
\(\overrightarrow{BD}.\overrightarrow{BC}\)
\(\overrightarrow{AC}.\overrightarrow{BD}\)
b)gọi I là trung điểm của CD tính \(\overrightarrow{AI.}\overrightarrow{BD}\)và suy ra góc của 2 vecto AI và BD
Câu 38. Cho tam giác ABC. Tìm tập hợp điểm M thỏa mãn 3|MA+MB| 2 |MA+ MB + MC| Câu 37. Trong mặt phẳng Oxy, cho tam giác ABC, có A(1;5), B(-2;2), C(3; - 1) . a. Tìm tọa độ điểm D sao cho ABCD là hình bình hành. b. Tìm tọa độ điểm E sao cho A là trung điểm đoạn BE. c. Tìm tọa độ điểm F sao cho B là trọng tâm tam giác ACF.
Đọc tiếp
Câu 38. Cho tam giác ABC. Tìm tập hợp điểm M thỏa mãn 3|MA+MB| =2 |MA+ MB + MC| Câu 37. Trong mặt phẳng Oxy, cho tam giác ABC, có A(1;5), B(-2;2), C(3; - 1) . a. Tìm tọa độ điểm D sao cho ABCD là hình bình hành. b. Tìm tọa độ điểm E sao cho A là trung điểm đoạn BE. c. Tìm tọa độ điểm F sao cho B là trọng tâm tam giác ACF.
Cho hình bình hành ABCD,có tâm O:
a) Tìm điểm I thỏa đẳng thức vecto: IA+IB+IC=BC
b) Gọi M nằm trên cạnh DC sao cho 2DM=MC.Biểu diễn OM theo 2 vecto AB và AD










