Chương 2: TÍCH VÔ HƯỚNG CỦA HAI VECTƠ VÀ ỨNG DỤNG
Các câu hỏi tương tự
Cho tứ giác ABCD nội tiếp (O;R). AC vuông góc với BD và AC cắt BD tại I. Gọi trung điểm của AB là M. Chứng minh rằng MI vuông góc với DC
Cho hình bình hành ABCD. Gọi O là giao điểm của hai đường chéo AC và BD; N là trung điểm của cạnh CD; P là điểm thỏa mãn hệ thức (1.0 điểm). Chứng minh đẳng thức .
Đọc tiếp
Cho hình bình hành ABCD. Gọi O là giao điểm của hai đường chéo AC và BD; N là trung điểm của cạnh CD; P là điểm thỏa mãn hệ thức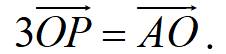
(1.0 điểm). Chứng minh đẳng thức .
Cho hình chữ nhật ABCD. Gọi E là hình chiếu cuarB trên AC, F và G là trung điểm của AE và CD. Chứng minh BF vuông góc với FG
cho hình vuông ABCD cạnh a . G ọi N là trung điểm của CD , M là điểm trên AC sao cho AM = \(\frac{1}{4}\) AC : a) tính các cạnh của tam giác BMN ; b) có nhận xét gì về tam giác BMN ? tính diện tích tam giác đó ; c) gọi I là giao điểm của BN và AC , tính CI ; d) tính bán kính đường tròn ngoại tiếp tam giác BDN
cho ΔABC cân tại A. H là trung điểm BC, D là hình chiếu của H trên AC, M là trung điểm HD. Chứng minh AM vuông góc BD
giúp mình bài này với
cho tứ giác ABCD, gọi M,N,P,Q lần lượt là trung điểm của AB,CD,BC,DA thỏa mãn điều kiện MN+PQ=1/2(AB+BC+CD+DA) thì ABCD là hình bình hành
cho hbh abcd gọi m n lần lượt là hai điểm nằm trên hai cạnh ab và cd sao cho ab =3AM CD=2CN Biểu diễn vectơ AN qua các vectơ AB và AC
Cho tam giác ABC, M là trung điểm của AB, N ϵ AC sao cho NC=2NA. Xác định D sao cho 3 véc tơ AB + 4 lần véc tơ AC - 12 lần véc tơ KD = véc tơ 0
cho tam giác ABC gọi K là điểm xác định bởi ( 2vectoKA+3vectoKB+vectoKC=vecto0) .gọi M,N là hai điểm phân biệt thõa mãn ( vectoMN= 2vectoMA+3vectoMB+vectoMC) chứng minh M,N luôn đi qua một điểm có định









