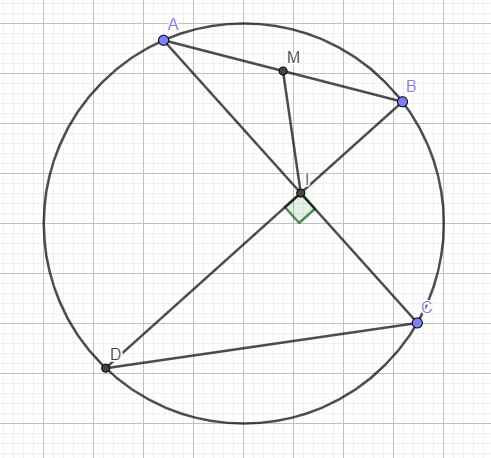
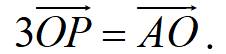M là trung điểm AB \(\Rightarrow\overrightarrow{IM}=\dfrac{1}{2}\left(\overrightarrow{IA}+\overrightarrow{IB}\right)\)
\(\Rightarrow2\overrightarrow{IM}.\overrightarrow{DC}=\left(\overrightarrow{IA}+\overrightarrow{IB}\right).\left(\overrightarrow{DI}+\overrightarrow{IC}\right)=\overrightarrow{IA}.\overrightarrow{DI}+\overrightarrow{IB}.\overrightarrow{IC}+\overrightarrow{IA}.\overrightarrow{IC}+\overrightarrow{IB}.\overrightarrow{DI}\)
\(=\overrightarrow{IA}.\overrightarrow{IC}+\overrightarrow{IB}.\overrightarrow{DI}=-IA.IC+IB.DI\)
Mặt khác do 2 tam giác vuông DIC và AIB đồng dạng (\(\widehat{IAB}=\widehat{IDC}\) cùng chắn BC)
\(\Rightarrow\dfrac{IA}{ID}=\dfrac{IB}{IC}\Rightarrow IA.IC=IB.ID\Rightarrow-IA.IC+IB.ID=0\)
\(\Rightarrow2\overrightarrow{IM}.\overrightarrow{DC}=0\Rightarrow IM\perp DC\)