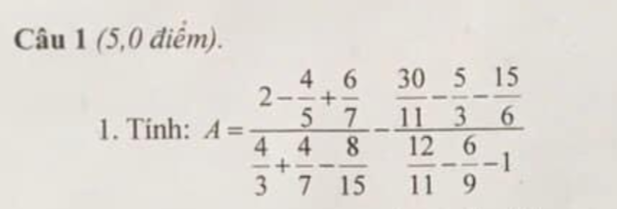\(A=\dfrac{\left(2^2\right)^6.\left(3^2\right)^5+6^9.6.20}{\left(2^3\right)^4.3^{12}-6^{11}}=\dfrac{2^{12}.3^{10}+6^{10}.20}{2^{12}.3^{12}-6^{11}}\)
\(A=\dfrac{2^2.2^{10}.3^{10}+6^{10}.20}{6^{12}-6^{11}}=\dfrac{4.6^{10}+6^{10}.20}{6^{12}-6^{11}}=\dfrac{6^{10}\left(4+20\right)}{6^{11}\left(6-1\right)}\)
\(A=\dfrac{6^{10}.24}{6^{11}.5}=\dfrac{6^{10}.6.4}{6^{11}.5}=\dfrac{6^{11}.4}{6^{11}.5}=\dfrac{4}{5}\)