Do n lẻ, đặt \(n=2m+1\)
\(\Rightarrow S=C_{2m+1}^1+C_{2m+1}^2+...+C_{2m+1}^m\)
Áp dụng đẳng thức: \(C_n^k=C_n^{n-k}\)
\(\Rightarrow S=C_{2m+1}^{2m}+C_{2m+1}^{2m-1}+...+C_{2m+1}^{m+1}\)
\(\Rightarrow2S=S+S=C_{2m+1}^1+C_{2m+1}^2+...+C_{2m+1}^{2m}\)
\(=C_{2m+1}^0+C_{2m+1}^1+...+C_{2m+1}^{2m+1}-\left(C_{2m+1}^0+C_{2m+1}^{2m+1}\right)\)
\(=2^{2m+1}-2\)
\(\Rightarrow S=2^{2m}-1\) luôn lẻ (đpcm)







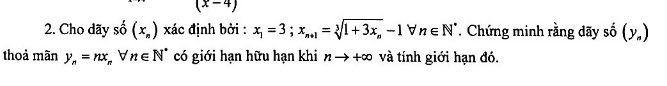

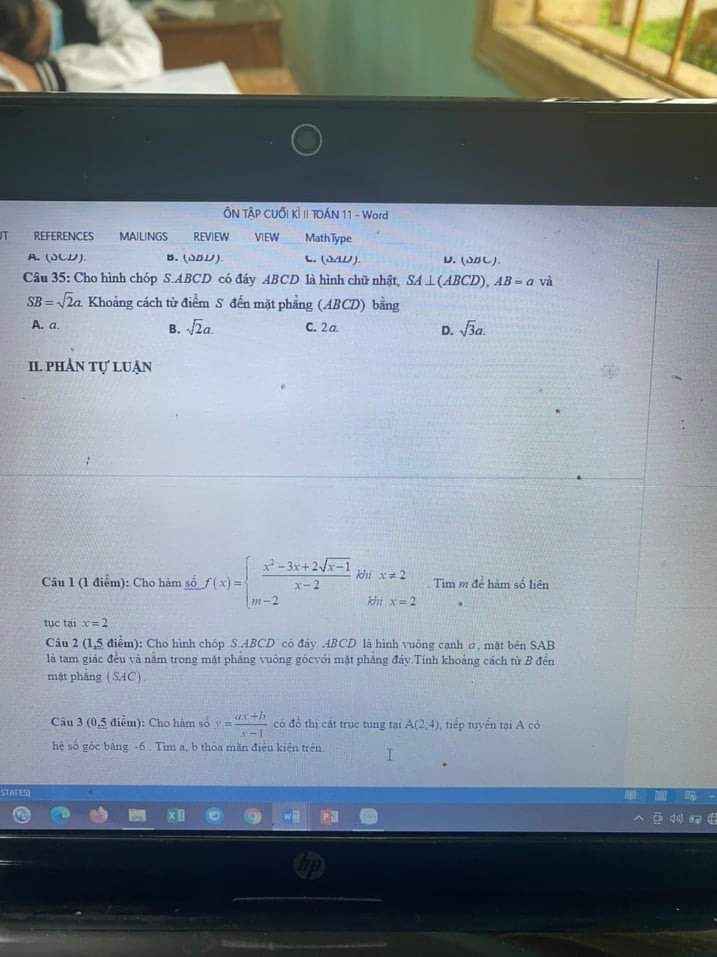

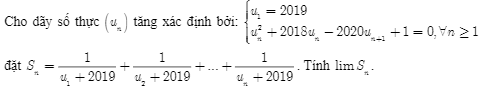
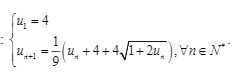 giúp em với mọi người ơi:(
giúp em với mọi người ơi:(
