Do \(\left(u_n\right)\) là dãy tăng nên \(u_n\ge2018,\forall n\ge1\)
Ta có : \(u^2_n+2018u_n-2020u_{n+1}=0\) \(\Leftrightarrow u_{n+1}=\dfrac{u^2_n+2018u_n+1}{2020}\)
\(\Leftrightarrow u_{n+1}-1=\dfrac{u^2_n+2018u_n-2019}{2020}\Leftrightarrow2020\left(u_{n+1}-1\right)=\left(u_n-1\right)\left(u_n+2019\right)\)
\(\Leftrightarrow\dfrac{2020}{\left(u_n-1\right)\left(u_n+2019\right)}=\dfrac{1}{u_{n+1}-1}\Rightarrow\dfrac{1}{u_n+2019}=\dfrac{1}{u_n-1}-\dfrac{1}{u_{n+1}-1}\left(1\right)\)
Thay n bởi 1 , 2, 3 , ..... , n vào (1) và cộng vế với vế các đẳng thức ta suy ra:
\(S_n=\dfrac{1}{u_1+2019}+\dfrac{1}{u_2+2019}+...+\dfrac{1}{u_n+2019}\)
\(=\dfrac{1}{u_1-1}-\dfrac{1}{u_{n+1}-1}=\dfrac{1}{2018}-\dfrac{1}{u_{n+1}-1}\)
Do \(\left(u_n\right)\) là dãy số tăng nên có 2 trường hợp xảy ra:
th1:
Dãy \(\left(u_n\right)\) bị chặn trên suy ra tồn tại \(lim\) \(u_n\) . Giả sử lim \(u_n\) = x thì \(x\ge2018\)
chuyển qua giới hạn hệ thức \(\left(1\right)khi\) \(n\rightarrow+\infty\) , ta có:
\(x^2+2018x-2020x+1=0\)
\(\Leftrightarrow x^2-2x+1=0\Leftrightarrow x=1\) ( điều này vô lý)
Dãy \(\left(u_n\right)\) ko bị chặn trên , do \(\left(u_n\right)\) tăng và ko bị chặn nên:
\(lim\) \(u_n\)\(=+\infty\Rightarrow lim\left(u_{n+1}-1\right)=+\infty\Rightarrow lim\dfrac{1}{u_{n+1}-1}=0\)
Do vậy: \(limS_n=lim\left(\dfrac{1}{2018}-\dfrac{1}{u_{n+1}-1}\right)=\dfrac{1}{2018}\)
á cái này bt nek mak gõ hơi chậm nha nói trc cỡ 15p ms xog ó:>

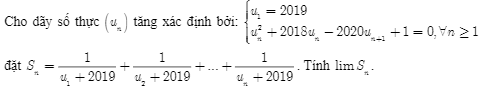






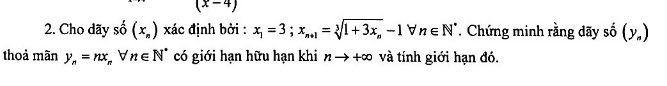



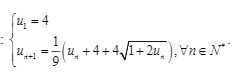 giúp em với mọi người ơi:(
giúp em với mọi người ơi:(