Ta dễ dàng quy nạp dãy \(u_n\) là dãy dương
Từ đó: \(u_n-u_{n-1}=u_{n-1}^2+u_{n-1}>0\Rightarrow\) dãy tăng
\(u_n+1=\left(u_{n-1}+1\right)^2\)
Đặt \(u_n+1=v_n\Rightarrow v_1=u_1+1=2\)
\(v_n=v_{n-1}^2=v_{n-2}^{2^2}=v_{n-3}^{2^3}=...=v_1^{2^{n-1}}=2^{2^{n-1}}\)
\(\Rightarrow u_n=v_n-1=2^{2^{n-1}}-1\)
\(u_1=1>0\)
\(u_2=u_1^2+2u_1=3>0\)
Giả sử \(u_k>0\) , ta cần chứng minh \(u_{k+1}>0\)
Hiển nhiên có \(u_{k+1}=u_k^2+2u_k>0^2+2.0=0\)







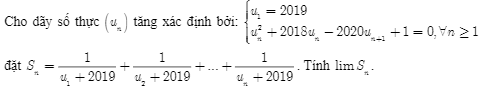
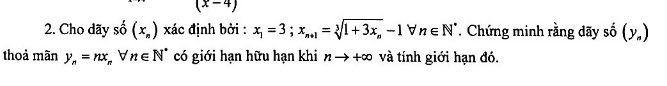



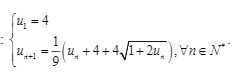 giúp em với mọi người ơi:(
giúp em với mọi người ơi:(