1.
\(\lim\limits_{x\rightarrow2}f\left(x\right)=\lim\limits_{x\rightarrow2}\dfrac{x^2-3x+2\sqrt{x-1}}{x-2}\)
\(=\lim\limits_{x\rightarrow2}\dfrac{x^2-3x+2+2\left(\sqrt{x-1}-1\right)}{x-2}\)
\(=\lim\limits_{x\rightarrow2}\dfrac{\left(x-1\right)\left(x-2\right)+\dfrac{2\left(x-2\right)}{\sqrt{x-1}+1}}{x-2}\)
\(=\lim\limits_{x\rightarrow2}\left(x-1+\dfrac{2}{\sqrt{x-1}+1}\right)=2\)
\(f\left(2\right)=m-2\)
Hàm liên tục tại \(x=2\) khi \(\lim\limits_{x\rightarrow2}f\left(x\right)=f\left(2\right)\)
\(\Leftrightarrow m-2=2\Rightarrow m=4\)
2.
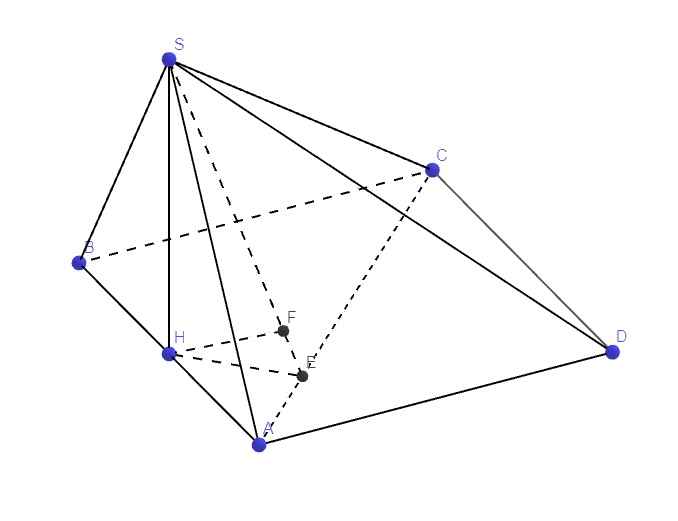
Gọi H là trung điểm AB \(\Rightarrow SH\perp AB\)
Mà \(\left\{{}\begin{matrix}AB=\left(ABCD\right)\cap\left(SAB\right)\\\left(ABCD\right)\perp\left(SAB\right)\end{matrix}\right.\) \(\Rightarrow SH\perp\left(ABCD\right)\)
Ta có: \(\left\{{}\begin{matrix}BH\cap\left(SAC\right)=A\\BA=2HA\end{matrix}\right.\)
\(\Rightarrow d\left(B;\left(SAC\right)\right)=2d\left(H;\left(SAC\right)\right)\)
Từ H kẻ \(HE\perp AC\)
\(SH\perp\left(ABCD\right)\Rightarrow SH\perp AC\)
\(\Rightarrow AC\perp\left(SHE\right)\Rightarrow\left(SAC\right)\perp\left(SHE\right)\)
Từ H kẻ \(HF\perp SE\Rightarrow HF\perp\left(SAC\right)\)
\(\Rightarrow HF=d\left(H;\left(SAC\right)\right)\)
\(ABCD\) là hình vuông \(\Rightarrow\widehat{HAE}=45^0\Rightarrow\Delta AHE\) vuông cân tại E
\(\Rightarrow HE=\dfrac{AH}{\sqrt{2}}=\dfrac{AB}{2\sqrt{2}}=\dfrac{a\sqrt{2}}{4}\)
\(SH=\dfrac{a\sqrt{3}}{2}\) (trung tuyến tam giác đều cạnh a)
Hệ thức lượng cho tam giác vuông SHE:
\(\dfrac{1}{HF^2}=\dfrac{1}{SH^2}+\dfrac{1}{HE^2}\Rightarrow HF=\dfrac{SH.HE}{\sqrt{SH^2+HE^2}}=\dfrac{a\sqrt{21}}{14}\)
\(\Rightarrow d\left(B;\left(SAC\right)\right)=2HF=\dfrac{a\sqrt{21}}{7}\)
3.
Câu 3 đề bài sai từ điều cơ bản nhất: đồ thị cắt trục tung tại A nhưng điểm A không hề nằm trên trục tung. (để nằm trên trục tung thì tọa độ điểm A cần có hoành độ bằng 0)