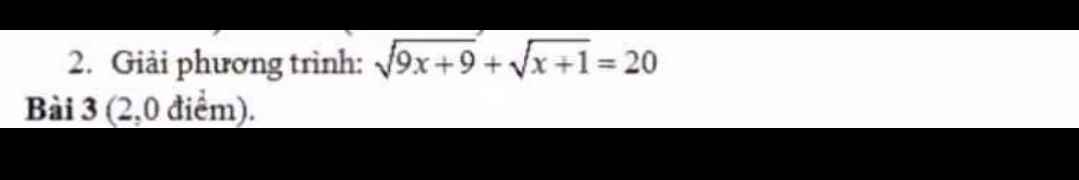\(ĐK:x\ge1\\ PT\Leftrightarrow3\sqrt{x+1}+\sqrt{x+1}=20\\ \Leftrightarrow\sqrt{x+1}=5\Leftrightarrow x+1=25\Leftrightarrow x=24\left(tm\right)\)
\(\sqrt{9x+9}+\sqrt{x+1}=20\left(đk:x\ge-1\right)\)
\(\Leftrightarrow3\sqrt{x+1}+\sqrt{x+1}=20\)
\(\Leftrightarrow4\sqrt{x+1}=20\Leftrightarrow\sqrt{x+1}=5\)
\(\Leftrightarrow x+1=25\Leftrightarrow x=24\left(tm\right)\)
ĐK: $x\ge -1$
$\sqrt{9x+9}+\sqrt{x+1}=20$
$\Leftrightarrow 3\sqrt{x+1}+\sqrt{x+1}=20$
$\Leftrightarrow 4\sqrt{x+1}=20$
$\Leftrightarrow \sqrt{x+1}=5$
$\Leftrightarrow x+1=25$
$\Leftrightarrow x=24(TM)$
\(\sqrt{9\left(x+1\right)}+\sqrt{x+1}=20\)
\(3\sqrt{x+1}+\sqrt{x+1}=20\)
\(4\sqrt{x+1}=20\)
\(\sqrt{x+1}=5\)
\(x+1=25\Leftrightarrow x=24\)
\(\sqrt{9x+9}+\sqrt{x+1}=20\)
Đk: x\(\ge\)-1
Pt: \(\Rightarrow3\sqrt{x+1}+\sqrt{x+1}=20\)
\(\Rightarrow\sqrt{x+1}=5\Rightarrow x+1=25\Rightarrow x=24\left(tmđk\right)\)
\(\sqrt{9\left(x+1\right)}+\sqrt{x+1}=\sqrt{9}\sqrt{x+1}+\sqrt{x+1}=3\sqrt{x+1}+\sqrt{x+1}=4\sqrt{x+1}\)