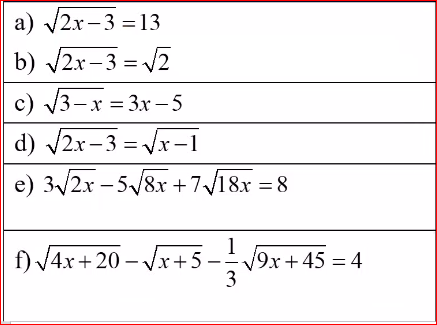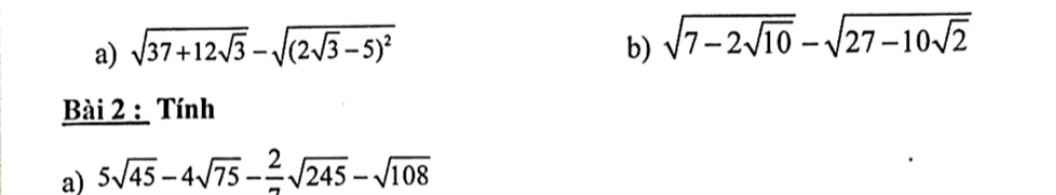\(e,3\sqrt{2x}-5\sqrt{8x}+7\sqrt{18x}=8\left(x\ge0\right)\\ \Leftrightarrow\sqrt{x}\left(3\sqrt{2}-5\sqrt{8}+7\sqrt{18}\right)=8\\ \Leftrightarrow\sqrt{x}\left(3\sqrt{2}-10\sqrt{2}+21\sqrt{2}\right)=8\\ \Leftrightarrow14\sqrt{2x}=8\Leftrightarrow\sqrt{2x}=\dfrac{4}{7}\Leftrightarrow2x=\dfrac{16}{49}\Leftrightarrow x=\dfrac{8}{49}\left(tm\right)\)
\(f,\sqrt{4x+20}-\sqrt{x+5}-\dfrac{1}{3}\sqrt{9x+45}=4\left(x\ge-5\right)\\ \Leftrightarrow2\sqrt{x+5}-\sqrt{x+5}-\dfrac{1}{3}\cdot3\sqrt{x+5}=4\\ \Leftrightarrow0\sqrt{x+5}=4\\ \Leftrightarrow\sqrt{x+5}=0\Leftrightarrow x+5=0\Leftrightarrow x=-5\left(tm\right)\)
e) \(3\sqrt{2x}-5\sqrt{8x}+7\sqrt{18x}=8\left(đk:x\ge0\right)\)
\(\Leftrightarrow3\sqrt{2x}-10\sqrt{2x}+21\sqrt{2x}=8\)
\(\Leftrightarrow14\sqrt{2x}=8\Leftrightarrow\sqrt{2x}=\dfrac{8}{14}\Leftrightarrow2x=\dfrac{16}{49}\Leftrightarrow x=\dfrac{8}{49}\left(tm\right)\)
f) \(\sqrt{4x+20}-\sqrt{x+5}-\dfrac{1}{3}\sqrt{9x+45}=4\)
\(\Leftrightarrow2\sqrt{x+5}-\sqrt{x+5}-\sqrt{x+5}=4\)
\(\Leftrightarrow0=4\left(VLý\right)\)
Vậy \(x\in\left\{\varnothing\right\}\)