8.
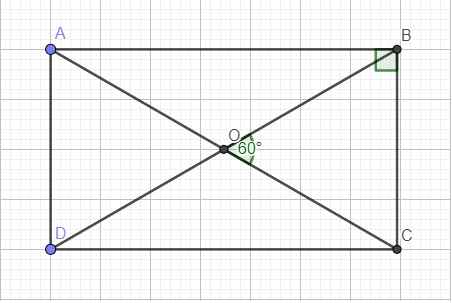
Đặt hình chữ nhật là ABCD với \(BD=AC=2\left(m\right)\), O là giao điểm 2 đường chéo \(\Rightarrow\widehat{BOC}=60^0\)
Ta có: \(\left\{{}\begin{matrix}OB=\dfrac{1}{2}BD=1\\OC=\dfrac{1}{2}AC=1\\\end{matrix}\right.\) \(\Rightarrow\Delta BOC\) cân tại O
\(\Rightarrow\Delta BOC\) là tam giác đều (tam giác cân có 1 góc bằng \(60^0\))
\(\Rightarrow BC=OB=OC=1\)
Áp dụng định lý Pitago trong tam giác vuông ABC:
\(AB=\sqrt{AC^2-BC^2}=\sqrt{2^2-1^2}=\sqrt{3}\left(m\right)\)
Vậy \(AD=BC=1\left(m\right)\) ; \(AB=CD=\sqrt{3}\left(m\right)\)
10.
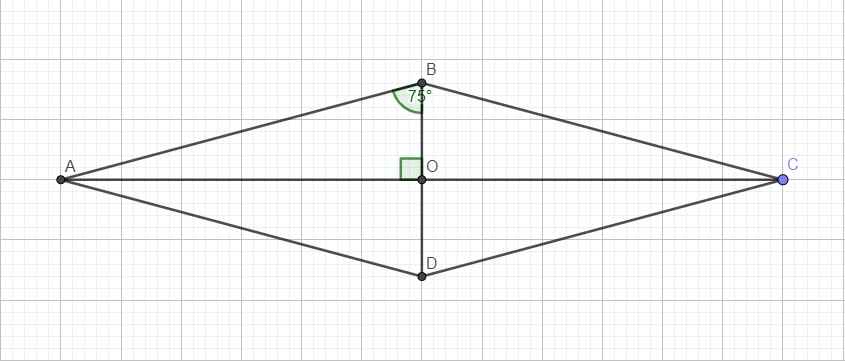
Giả sử hình thoi ABCD với cạnh 10cm và \(\widehat{ABC}=150^0\)
Do ABCD là hình thoi \(\Rightarrow AC\perp BD\)
Gọi O là giao điểm 2 đường chéo \(\Rightarrow\Delta OAB\) vuông tại O đồng thời BO là tia phân giác góc \(\widehat{ABC}\)
\(\Rightarrow\widehat{ABO}=\dfrac{1}{2}\widehat{ABC}=75^0\)
Trong tam giác vuông OAB ta có:
\(sin\widehat{ABO}=\dfrac{AO}{AB}\Rightarrow AO=AB.sin\widehat{ABO}=10.sin75^0\)
\(cos\widehat{ABO}=\dfrac{OB}{AB}\Rightarrow OB=AB.cos\widehat{ABO}=10.cos75^0\)
\(\Rightarrow AC=2AO=20.sin75^0\approx19,3\left(cm\right)\)
\(BD=2OB=20.cos75^0\approx5,2\left(cm\right)\)