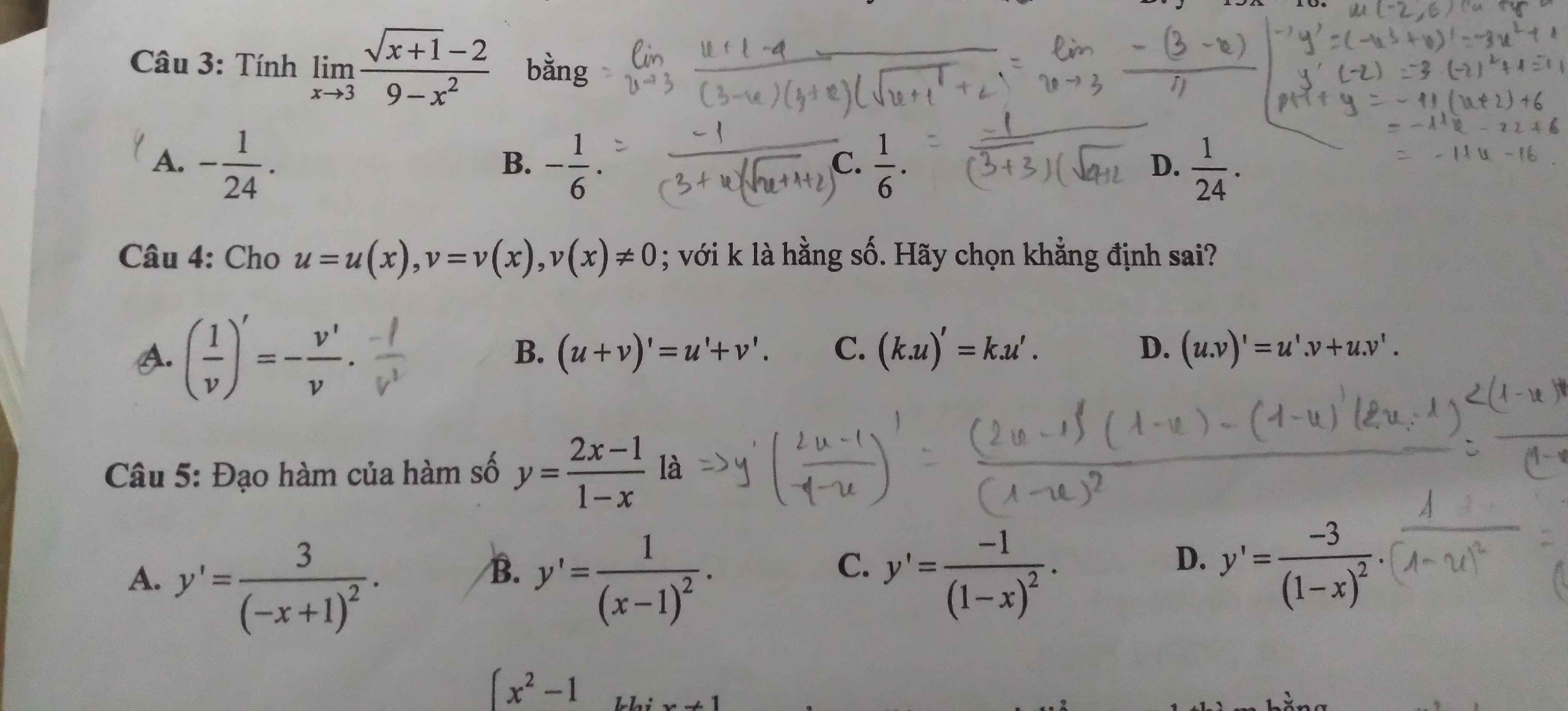3.
\(\lim\limits_{x\rightarrow3}\dfrac{\sqrt{x+1}-2}{9-x^2}=\lim\limits_{x\rightarrow3}\dfrac{x-3}{-\left(x-3\right)\left(x+3\right)\left(\sqrt{x+1}+2\right)}\)
\(=\lim\limits_{x\rightarrow3}\dfrac{-1}{\left(x+3\right)\left(\sqrt{x+1}+2\right)}=\dfrac{-1}{6.\left(2+2\right)}=-\dfrac{1}{24}\)
4.
A là khẳng định sai
\(\left(\dfrac{1}{v}\right)'=-\dfrac{v'}{v^2}\) mới là công thức đạo hàm đúng
5.
\(y'=\dfrac{\left(2x-1\right)'\left(1-x\right)-\left(1-x\right)'\left(2x-1\right)}{\left(1-x\right)^2}=\dfrac{2\left(1-x\right)+\left(2x-1\right)}{\left(1-x\right)^2}\)
\(=\dfrac{1}{\left(1-x\right)^2}=\dfrac{1}{\left(x-1\right)^2}\)
Đúng 0
Bình luận (0)
