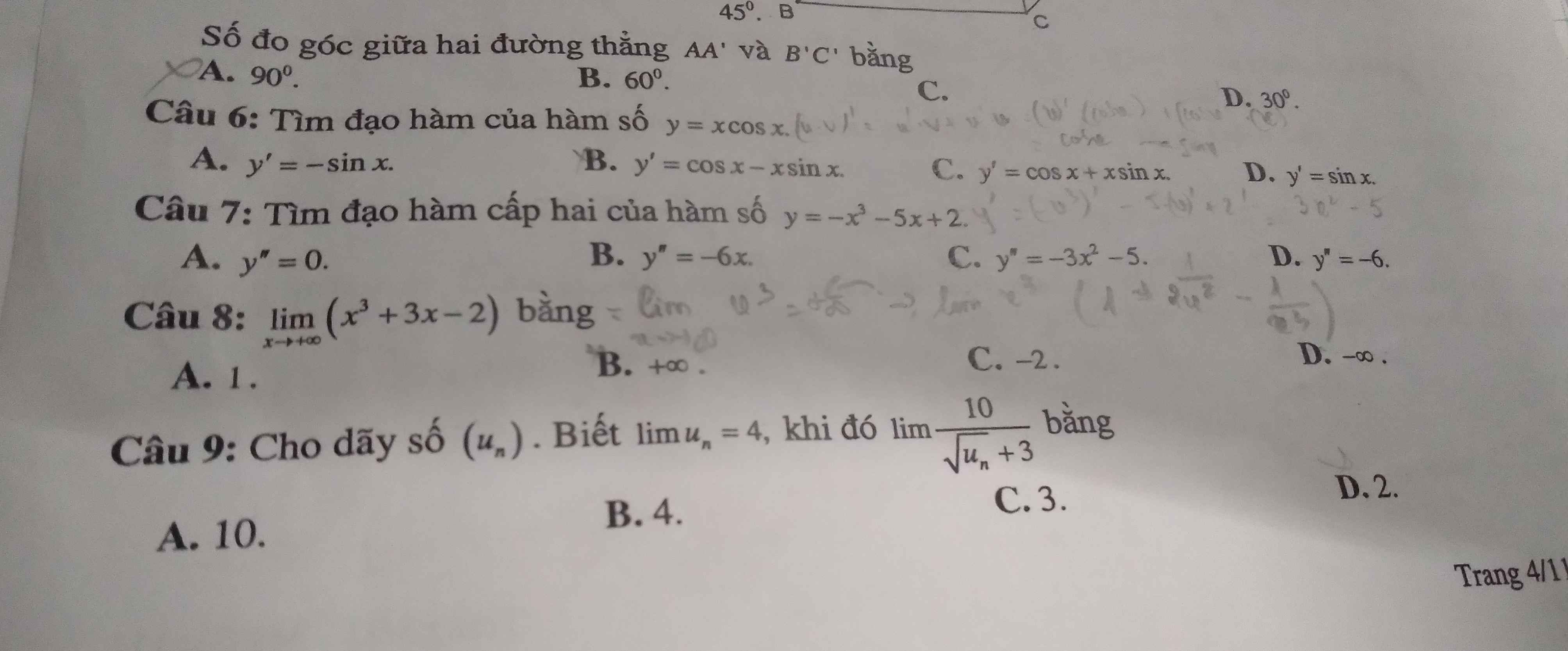Question

Giúp e giải chỉ tiết câu 7 , 8 đi mọi người

Answer 1

7.

\(y'=\left(-x^3\right)'-\left(5x\right)'+\left(2\right)'=-3x^2-5\)

\(y''=\left(-3x^2\right)'-\left(5\right)'=-6x\)

8.

\(\lim\limits_{x\rightarrow+\infty}\left(x^3+3x-2\right)=\lim\limits_{x\rightarrow+\infty}x^3\left(1+\dfrac{3}{x^2}-\dfrac{2}{x^3}\right)\)

Do: \(\lim\limits_{x\rightarrow+\infty}x^3=+\infty\)

\(\lim\limits_{x\rightarrow+\infty}\left(1+\dfrac{3}{x^2}-\dfrac{2}{x^3}\right)=1>0\)

\(\Rightarrow\lim\limits_{x\rightarrow+\infty}x^3\left(1+\dfrac{3}{x^2}-\dfrac{2}{x^3}\right)=+\infty\)