-Hình vẽ:
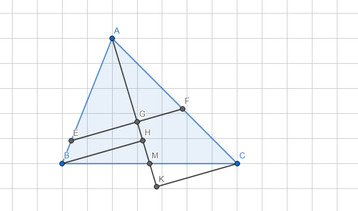
*Qua B,C kẻ các đường thẳng song song với EF cắt AG lần lượt tại H,K.
*AG cắt BC tại M.
- Xét △ABC có: G là trọng tâm (gt).
=>AG là trung tuyến của △ABC.
Mà AG cắt BC tại M (gt).
=>M là trung điểm BC; \(AG=2GM\)
- Ta có: \(BH\)//\(EF\) (gt) ; \(CK\)//\(EF\) (gt).
=>\(BH\)//\(CK\).
- Xét △BHM và △CKM có:
\(\widehat{BHM}=\widehat{CKM}\) (\(BH\)//\(CK\) và so le trong).
\(BM=CM\) (M là trung điểm BC).
\(\widehat{BMH}=\widehat{CMK}\) (đối đỉnh).
=>△BHM = △CKM (c-g-c).
=>\(HM=KM\) (2 cạnh tương ứng).
*\(GH+GK=GM-HM+GM+MK=2GM=AG\).
- Xét △ABH có: \(EG\)//\(BH\) (gt).
=>\(\dfrac{BE}{AE}=\dfrac{GH}{AG}\) (định lí Ta-let). (1).
- Xét △ACK có: \(GF\)//\(CK\) (gt).
=>\(\dfrac{CF}{AF}=\dfrac{GK}{AG}\) (định lí Ta-let) (2).
- Từ (1) và (2) suy ra:
\(\dfrac{BE}{AE}+\dfrac{CF}{AF}=\dfrac{GH}{AG}+\dfrac{GK}{AG}=\dfrac{AG}{AG}=1\).