a.f(x)=x.(2x^3-x^2+4x-1) =>f(x)=2x^4-x^3+4x^2-x f'(x)=(2x^4-x^3+4x^2-x)’ => f'(x)= 8x^3-3x^2-8x-1
a.
\(f\left(x\right)=2x^4-x^3+4x^2-x\)
\(\Rightarrow f'\left(x\right)=8x^3-3x^2+8x-1\)
b.
\(f'\left(x\right)=\left(2x\right)'.sinx+2x.\left(sinx\right)'=2sinx+2x.cosx\)
c.
\(f\left(x\right)=3x+2-\dfrac{5}{x}\Rightarrow f'\left(x\right)=3+\dfrac{5}{x^2}=\dfrac{3x^2+5}{x^2}\)

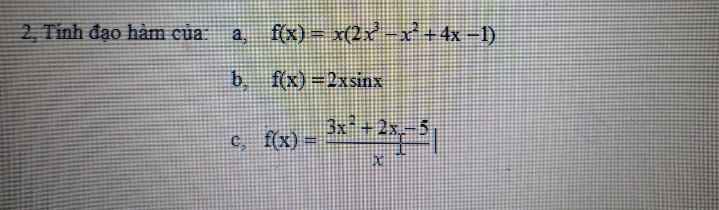




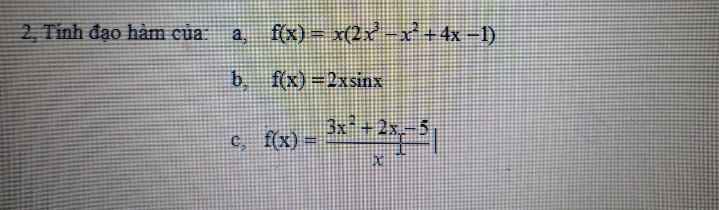






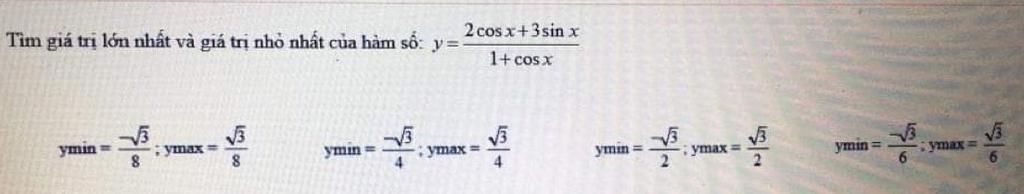



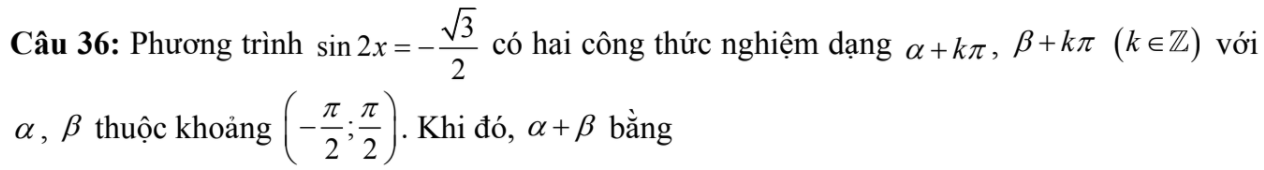 giúp mk với ạ
giúp mk với ạ
